题目内容
8.函数y=loga(x+2)-1(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m>0,n>0,则$\frac{1}{m}$+$\frac{2}{n}$的最小值为( )| A. | 3+2$\sqrt{2}$ | B. | 3+2$\sqrt{3}$ | C. | 7 | D. | 11 |
分析 函数y=loga(x+2)-1(a>0,a≠1)的图象恒过定点A(-1,-1),可得m+n=1.于是$\frac{1}{m}$+$\frac{2}{n}$=(m+n)$(\frac{1}{m}+\frac{2}{n})$=3+$\frac{n}{m}$+$\frac{2m}{n}$,再利用基本不等式的性质即可得出.
解答 解:函数y=loga(x+2)-1(a>0,a≠1)的图象恒过定点A(-1,-1),
∵点A在直线mx+ny+1=0上,其中m>0,n>0,∴-m-n+1=0,即m+n=1.
则$\frac{1}{m}$+$\frac{2}{n}$=(m+n)$(\frac{1}{m}+\frac{2}{n})$=3+$\frac{n}{m}$+$\frac{2m}{n}$≥3+2$\sqrt{\frac{n}{m}•\frac{2m}{n}}$=3+2$\sqrt{2}$,当且仅当n=$\sqrt{2}$m=2-$\sqrt{2}$时取等号.
故选:A.
点评 本题考查了对数函数的性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
18. 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )| A. | $\frac{5}{4}$ | B. | $\frac{24}{7}$ | C. | $-\frac{21}{24}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
3.a,b为正实数,若函数f(x)=ax3+bx+ab-1是奇函数,则f(2)的最小值是( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
13.已知向量$\overrightarrow{a}$=(-2,0),$\overrightarrow{b}$=(1,1),则下列结论正确的是( )
| A. | $\overrightarrow{a}$•$\overrightarrow{b}$=2 | B. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | C. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D. | $\overrightarrow{b}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$) |
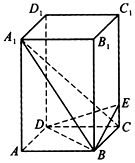 如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1
如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1 如图所示的几何体P-ABCD中,四边形ABCD为菱形,∠ABC=120°,AB=a,$PB=\sqrt{3}a$,PB⊥AB,平面ABCD⊥平面PAB,AC∩BD=O,E为PD的中点,G为平面PAB内任一点.
如图所示的几何体P-ABCD中,四边形ABCD为菱形,∠ABC=120°,AB=a,$PB=\sqrt{3}a$,PB⊥AB,平面ABCD⊥平面PAB,AC∩BD=O,E为PD的中点,G为平面PAB内任一点.