题目内容
已知首项为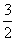
的等比数列{an}的前n项和为Sn(n∈N*), 且－2S2，S3,4S4成等差数列．
(1)求数列{an}的通项公式；
(2) 证明Sn＋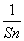
≤
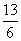(n∈N*)．
(1)解析：设等比数列{an}的公比为q，因为－2S2，S3,4S4成等差数列，所以S3＋2S2＝4S4－S3，即S4－S3＝S2－
S4，可得2a4＝－a3，于是q＝
＝－
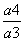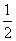，又a1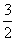＝，所以等比数列{an}的通项公式为an＝×
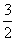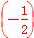n－1＝(－1)n－1·
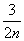(n∈N*)．
(2)证明：Sn＝1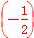－n，
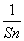Sn＋＝1－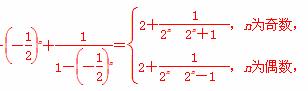
当n为奇数时，Sn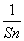＋随n的增大而减小，所以Sn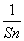＋≤S1＋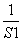
＝.
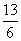当n为偶数时，Sn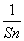＋随n的增大而减小，所以Sn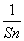＋≤S2＋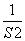
＝
.
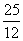练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
，若对任意的n∈N*都有an≥a5，则实数b的取值范围是__________．
数f(x)＝
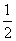x2＋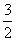
x，数列{an}的前n项和为Sn，点(n，Sn)(n∈N*)均在函数y＝f(x)的图象上，则数列{an}的通项公式an＝__________.
列{bn}是首项为a1，公差为d(d≠0)的等差数列，且b1，b3，b11成等比数列．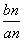
，求数列{cn}的前n项和Tn.
B．±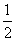
x＋b与曲线y＝－
sinx＋cosx，则f(
)＝________.
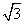|b|，若函数f(x)＝
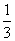x3＋|a|x2＋2a·bx＋1在R上有极值，则〈a，b〉的取值范围是( )
] B．(0，
]
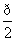] D．(