题目内容
已知非零向量a、b满足|a|=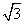 |b|,若函数f(x)=
|b|,若函数f(x)=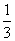 x3+|a|x2+2a·bx+1在R上有极值,则〈a,b〉的取值范围是( )
x3+|a|x2+2a·bx+1在R上有极值,则〈a,b〉的取值范围是( )
A.[0, ] B.(0,
] B.(0, ]
]
C.( ,
,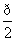 ] D.(
] D.( ,π]
,π]
D
[解析] 据题意知,f ′(x)=x2+2|a|x+2a·b,若函数存在极值,必有(2|a|)2-4×2a·b>0,整理可得|a|2>2a·b,故cos〈a,b〉= =
= ,解得
,解得 <〈a,b〉≤π.
<〈a,b〉≤π.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
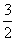 的等比数列{an}的前n项和为Sn(n∈N*), 且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*), 且-2S2,S3,4S4成等差数列.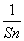 ≤
≤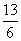 (n∈N*).
(n∈N*).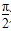 )上不是凸函数的是________(把你认为正确的序号都填上).
)上不是凸函数的是________(把你认为正确的序号都填上). (m∈R)在区间[1,e]上取得最小值4,则m=________.
(m∈R)在区间[1,e]上取得最小值4,则m=________. R D.
R D. R
R ,当
,当 时,
时, ;当
;当 时,
时, .
. 、
、 的值;
的值; ,且
,且 ,求
,求 的取值范围;
的取值范围; ,当
,当 取何值时,对
取何值时,对 ,函数
,函数 的值恒为负数?
的值恒为负数?