题目内容
某象棋比赛规则如下:两名选手比赛时,每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时结束.假设选手甲与选手乙比赛时,甲、乙每局获胜的概率分别为
和
,且各局比赛胜负互不影响.
(1)求比赛进行4局结束,且乙比甲多得2分的概率;
(2)设ξ表示比赛停止时已比赛的局数,求随机变量ξ的分布列和数学期望.
| 2 |
| 3 |
| 1 |
| 3 |
(1)求比赛进行4局结束,且乙比甲多得2分的概率;
(2)设ξ表示比赛停止时已比赛的局数,求随机变量ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差
专题:应用题,概率与统计
分析:(1)比赛进行4局结束,且乙比甲多得2分,即头两局乙胜一局,3、4局连胜,利用相互独立性概率公式,可得结论;
(2)随机变量ξ可能的取值为2,4,6,求出相应的概率,可得ξ的分布列和数学期望.
(2)随机变量ξ可能的取值为2,4,6,求出相应的概率,可得ξ的分布列和数学期望.
解答:
解:(1)比赛进行4局结束,且乙比甲多得2分,即头两局乙胜一局,3、4局连胜,
则所求概率为P=
•
•
•
•
=
;
(2)由题意,ξ的取值为2,4,6,则
P(ξ=2)=(
)2+(
)2=
,P(ξ=4)=
•
•
•(
)2+
•
•
•(
)2=
P(ξ=6)=(
•
•
)2=
,
∴ξ的分布列
数学期望Eξ=2×
+4×
+6×
=
.
则所求概率为P=
| C | 1 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 81 |
(2)由题意,ξ的取值为2,4,6,则
P(ξ=2)=(
| 2 |
| 3 |
| 1 |
| 3 |
| 5 |
| 9 |
| C | 1 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| C | 1 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 20 |
| 81 |
P(ξ=6)=(
| C | 1 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 81 |
∴ξ的分布列
| ξ | 2 | 4 | 6 | ||||||
| P |
|
|
|
| 5 |
| 9 |
| 20 |
| 81 |
| 16 |
| 81 |
| 266 |
| 81 |
点评:本题考查概率知识,考查离散型随机变量的分布列与数学期望,确定变量的取值,正确求概率是关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知sinθ<0,tanθ>0,则
化简的结果为( )
| ||
| cosθ |
| A、1 | B、-1 |
| C、±1 | D、以上都不对 |
已知向量
=(-1,2),
=(3,m),
∥(
+
),则m等于( )
| a |
| b |
| a |
| a |
| b |
| A、4 | B、3 | C、-4 | D、-6 |
已知函数y=f(x)是定义在R上的奇函数,且f′(x)-f(x)>0(其中f′(x)是f(x)的导函数)恒成立.若a=
,b=
,c=-ef(1),则a,b,c的大小关( )
| f(ln3) |
| 3 |
| f(ln2) |
| 2 |
| A、a>b>c |
| B、c>a>b |
| C、c>b>a |
| D、a>c>b |
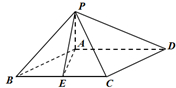 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,又PA⊥底面ABCD,AB=2PA,E为BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,又PA⊥底面ABCD,AB=2PA,E为BC的中点.