题目内容
14.执行如图的程序框图,输出的结果为( )
| A. | 136 | B. | 134 | C. | 268 | D. | 266 |
分析 执行程序框图,依次写出每次循环得到的S、i的值,即可求出程序运行后输出S的值.
解答 解:执行如图的程序框图,有
S=1,i=1
满足条件i>1,有S=1×8-2=6,i=6
满足条件i>1,有S=6×6-2=34,i=4
满足条件i>1,有S=34×4-2=134,i=2
满足条件i>1,有S=134×2-2=266,i=0
不满足条件i>1,输出S=266.
故选:D.
点评 本题考查了程序框图和算法的应用问题,是基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
2.已知双曲线C:$\frac{x^2}{{a{\;}^2}}-\frac{y^2}{{b{\;}^2}}$=1的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某一条渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$且$\overrightarrow{OQ}=5\overrightarrow{OP}$,则双曲线C的离心率为( )
| A. | 2 | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 3 |
6.已知$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,则$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
3.某供货商计划将某种大型节日商品分别配送到甲、乙两地销售.据以往数据统计,甲、乙两地该商品需求量的频率分布如下:
甲地需求量频率分布表示:
乙地需求量频率分布表:
以两地需求量的频率估计需求量的概率
(Ⅰ)若此供货商计划将10件该商品全部配送至甲、乙两地,为保证两地不缺货(配送量≥需求量)的概率均大于0.7,问该商品的配送方案有哪几种?
(Ⅱ)已知甲、乙两地该商品的销售相互独立,该商品售出,供货商获利2万元/件;未售出的,供货商亏损1万元/件.在(Ⅰ)的前提下,若仅考虑此供货商所获净利润,试确定最佳配送方案.
甲地需求量频率分布表示:
| 需求量 | 4 | 5 | 6 |
| 频率 | 0.5 | 0.3 | 0.2 |
| 需求量 | 3 | 4 | 5 |
| 频率 | 0.6 | 0.3 | 0.1 |
(Ⅰ)若此供货商计划将10件该商品全部配送至甲、乙两地,为保证两地不缺货(配送量≥需求量)的概率均大于0.7,问该商品的配送方案有哪几种?
(Ⅱ)已知甲、乙两地该商品的销售相互独立,该商品售出,供货商获利2万元/件;未售出的,供货商亏损1万元/件.在(Ⅰ)的前提下,若仅考虑此供货商所获净利润,试确定最佳配送方案.
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1和F2,以F1F2为直径的圆与双曲线的一个交点为P,若|PF1|=a,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\sqrt{10}$ | D. | $\sqrt{2}$ |
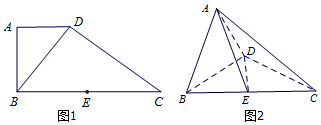 如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.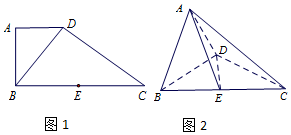 如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体
如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体