题目内容
9.已知f(x)=$\frac{{2+ln{x^2}}}{x}$.(1)求函数f(x)的单调区间;
(2)若不等式ex(2x3-3x2)-lnx-ax>1恒成立,求a的取值范围.
分析 (1)利用导函数的符号判断函数的单调性,求解单调区间即可.
(2)由不等式ex(2x3-3x2)-lnx-ax>1恒成立,得到${e^x}(2{x^2}-3x)-a>\frac{lnx+1}{x}$恒成立,设$g(x)={e^x}(2{x^2}-3x)-a,h(x)=\frac{lnx+1}{x}$,求出$g'(x)={e^x}(2{x^2}+x-3)={e^x}(2x+3)(x-1),h'(x)=\frac{-lnx}{x^2}$
利用函数的单调性求出函数的最值,即可求解a的范围.
解答 解:(1)由$f(x)=\frac{{2+ln{x^2}}}{x}$得:$f'(x)=\frac{{\frac{2}{x}x-2-ln{x^2}}}{x^2}=\frac{{-ln{x^2}}}{x^2}$
由于定义域为{x|x≠0},
所以由y'>0得:0<x<1或-1<x<0
所以由y'<0得:x<-1或x>1
即得函数在区间(0,1),(-1,0)上单调递增,在区间(-∞,-1),(1,+∞)上单调递减.
(2)由不等式ex(2x3-3x2)-lnx-ax>1恒成立,
即${e^x}(2{x^2}-3x)-a>\frac{lnx+1}{x}$恒成立
设$g(x)={e^x}(2{x^2}-3x)-a,h(x)=\frac{lnx+1}{x}$得:
$g'(x)={e^x}(2{x^2}+x-3)={e^x}(2x+3)(x-1),h'(x)=\frac{-lnx}{x^2}$,
因为它们的定义域(0,+∞),所以易得:
函数g(x)在(0,1)上单调递减,(1,+∞)上单调递增;
函数h(x)在(0,1)上单调递增,(1,+∞)上单调递减;
这两个函数在x=1处,g(x)有最小值,h(x)有最大值,
所以要使不等式${e^x}(2{x^2}-3x)-a>\frac{lnx+1}{x}$恒成立,
则只需满足$e(2-3)-a>\frac{ln1+1}{1}$,即a<-1-e.
点评 本题考查函数的导数的综合应用,函数的最值以及函数恒成立转化思想的应用,考查分析问题解决问题的能力.

 优等生题库系列答案
优等生题库系列答案(1)根据以上数据,完成下面的2×2列联表,并判断是否有90%的把握认为一孩或二孩宝宝的出生与医院有关?
| 一孩 | 二孩 | 合计 | |
| 人民医院 | |||
| 博爱医院 | |||
| 合计 |
附:${K^2}=\frac{{n{{({αb-bc})}^2}}}{{({α+b})({c+d})({α+c})({b+d})}}$
| P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
| A. | $({0,\frac{1}{8}}]$ | B. | $({0,\frac{5}{8}}]$ | C. | $({0,\frac{1}{8}}]∪[{\frac{5}{8},1}]$ | D. | $({0,\frac{1}{8}}]∪[{\frac{1}{4},\frac{5}{8}}]$ |

| A. | 136 | B. | 134 | C. | 268 | D. | 266 |
| A. | π | B. | $\frac{3π}{2}$ | C. | 2π | D. | 3π |
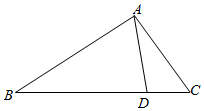 如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC
如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC