题目内容
若a＞b＞0，且a+b=1，则下列式子中最大的是（ ）
| A、log2a+log2b+1 |
| B、log2a |
| C、log2（a2+b2） |
| D、-1 |
考点：函数的最值及其几何意义,对数的运算性质
专题：不等式的解法及应用
分析：运用不等式的性质和基本不等式，也可以采用特殊值法，如：取a=0.6，b=0.4．
解答：
解：A：log2a+log2b+1=log22ab，D：-1=log2
，
∵a＞b＞0，且a+b=1，
∴a=a（a+b）=a2+ab＞a2+b2＞2ab，又a＞
，
∴log2a＞log2(a2+b2)＞log22ab，且log2a＞log2
=-1，
log2a最大．
故答案选择：B．
| 1 |
| 2 |
∵a＞b＞0，且a+b=1，
∴a=a（a+b）=a2+ab＞a2+b2＞2ab，又a＞
| 1 |
| 2 |
∴log2a＞log2(a2+b2)＞log22ab，且log2a＞log2
| 1 |
| 2 |
log2a最大．
故答案选择：B．
点评：本题考查不等式的性质和基本不等式的运用．属于基础题．
练习册系列答案
相关题目
设集合M={1，2，3}，N={x|log2x＞1），则M∩N=（ ）
| A、{3} |
| B、{2，3} |
| C、{1，3} |
| D、{1，2，3} |
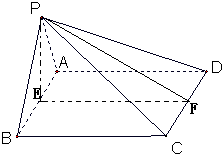如图，四棱锥P-ABCD的底面是矩形，侧面PAB是等边三角形，AB、CD中点分别为E、F，侧面PAB⊥底面ABCD．