题目内容
 某学校共有30至50岁之间的(包括30与不包括50)数学教师15人,其年龄分布茎叶图如图所示,从中选取3人参加支教.
某学校共有30至50岁之间的(包括30与不包括50)数学教师15人,其年龄分布茎叶图如图所示,从中选取3人参加支教.(Ⅰ)若教师年龄分布的极差为15,求教师的平均年龄;
(Ⅱ)若选出的3人中有2名男教师1名女教师,将他们分配到两所学校,每校至少有一人,则2名男教师分在同一所学校的概率为多少?
考点:列举法计算基本事件数及事件发生的概率,茎叶图
专题:概率与统计
分析:(1)根据极差的定义先求出x的值,再根据求平均数的公式求解即可;
(2)这是一个古典概型,列举出所有的基本事件,再找出2名男教师分在同一所学校的事件即可求出概率.
(2)这是一个古典概型,列举出所有的基本事件,再找出2名男教师分在同一所学校的事件即可求出概率.
解答:
解:(1)极差为15,所以40+x-30=15,所以x=5----------------(2分)
=
=37-----(4分)
(2)基本事件为:总数为6个---------------(7分)
2名男教师分在同一所学校所包含的基本事件的个数为2个----------------(9分)
2名男教师分在同一所学校的概率p=
=
----------------(12分)
. |
| x |
| 30+32+32+34+35+36+36+37+37+40+41+42+44+45 |
| 15 |
(2)基本事件为:总数为6个---------------(7分)
| 学校甲 | 学校乙 | ||||
| 男1男2 | 男1女 | 男2女 | 女 | 男2 | 男1 |
| 女 | 男2 | 男1 | 男1男2 | 男1女 | 男2女 |
2名男教师分在同一所学校的概率p=
| 2 |
| 6 |
| 1 |
| 3 |
点评:本题主要考查极差、平均数、古典概型等知识,属于基础题.

练习册系列答案
相关题目
设集合A={x|-1≤x<2},B={x|x>a},若A∩B≠∅,则a的取值范围是( )
| A、a<2 | B、a≤2 |
| C、a>-1 | D、-1<a≤2 |
已知函数f(x)=2x+sinx,若f(2x-y+3)≤0,则x2+y2的最小值为( )
A、
| ||||
B、3
| ||||
C、
| ||||
D、
|
函数f(x)=
x+log2x的零点所在区间为( )
| π |
| 2 |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
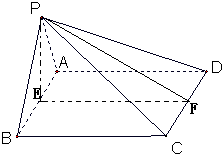 如图,四棱锥P-ABCD的底面是矩形,侧面PAB是等边三角形,AB、CD中点分别为E、F,侧面PAB⊥底面ABCD.
如图,四棱锥P-ABCD的底面是矩形,侧面PAB是等边三角形,AB、CD中点分别为E、F,侧面PAB⊥底面ABCD.