题目内容
已知函数f（x）对任意实数x1，x2都有f（x1x2）=f（x1）+f（x2）成立，则f（0）= ，f（1）= ．
考点：抽象函数及其应用
专题：计算题,函数的性质及应用
分析：由条件可令x1=x2=0，即可得到f（0）；再令x1=x2=1，即可得到f（1）．
解答：
解：由于f（x）对任意实数x1，x2都有f（x1x2）=f（x1）+f（x2）成立，
则可令x1=x2=0，则f（0）=f（0）+f（0），即有f（0）=0；
再令x1=x2=1，则f（1）=f（1）+f（1），即有f（1）=0．
故答案为：0，0
则可令x1=x2=0，则f（0）=f（0）+f（0），即有f（0）=0；
再令x1=x2=1，则f（1）=f（1）+f（1），即有f（1）=0．
故答案为：0，0
点评：本题考查抽象函数及应用，考查解决抽象函数的常用方法：赋值法，正确赋值是迅速解题的关键．
练习册系列答案
相关题目
设集合A={x|-1≤x＜2}，B={x|x＞a}，若A∩B≠∅，则a的取值范围是（ ）
| A、a＜2 | B、a≤2 |
| C、a＞-1 | D、-1＜a≤2 |
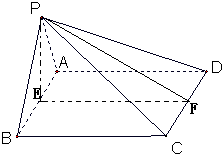如图，四棱锥P-ABCD的底面是矩形，侧面PAB是等边三角形，AB、CD中点分别为E、F，侧面PAB⊥底面ABCD．