题目内容
已知x∈{1，x2}，则实数x= ．
考点：元素与集合关系的判断
专题：集合
分析：由已知条件得：x=1，或x=x2，求出x并验证集合元素的互异性即可．
解答：
解：∵x∈{1，x2}；
∴若x=1，x2=1，则不满足集合元素的互异性，即x≠1；
若x=x2，解得x=0或1，由上面知x≠1，∴x=0；
综上得x=0．
故答案为：0．
∴若x=1，x2=1，则不满足集合元素的互异性，即x≠1；
若x=x2，解得x=0或1，由上面知x≠1，∴x=0；
综上得x=0．
故答案为：0．
点评：考查元素与集合的关系，集合元素的互异性．
练习册系列答案
相关题目
设集合M={1，2，3}，N={x|log2x＞1），则M∩N=（ ）
| A、{3} |
| B、{2，3} |
| C、{1，3} |
| D、{1，2，3} |
设集合A={x|-1≤x＜2}，B={x|x＞a}，若A∩B≠∅，则a的取值范围是（ ）
| A、a＜2 | B、a≤2 |
| C、a＞-1 | D、-1＜a≤2 |
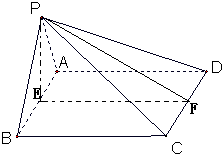如图，四棱锥P-ABCD的底面是矩形，侧面PAB是等边三角形，AB、CD中点分别为E、F，侧面PAB⊥底面ABCD．