题目内容
 在如图所示的几何体中,四边形ABDE为直角梯形,AE⊥AB,AE∥BD,AC⊥BC,AC=BC=BD=2AE=2,CE=
在如图所示的几何体中,四边形ABDE为直角梯形,AE⊥AB,AE∥BD,AC⊥BC,AC=BC=BD=2AE=2,CE=| 5 |
(1)求证:平面ABDE⊥平面ABC;
(2)求二面角D-CE-M的余弦值;
(3)求三棱锥D-CME的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定,用空间向量求平面间的夹角
专题:空间位置关系与距离
分析:(1)由勾股定理可得AE⊥AC,结合AE⊥AB和线面垂直的判定定理可得AE⊥平面ABC,进而由面面垂直的判定定理得到平面ABDE⊥平面ABC;
(2)解法一:连接DM,可证得DM⊥平面CME,过M作MF⊥CE交CE于点F,连接DF,则∠DFM即为二面角D-CE-M的平面角,解三角形求出答案;
解法二:以C为原点,CA,CB分别为x轴,y轴建立空间直角坐标系.计算出平面CDE的法向量和平面CEM的法向量,利用向量夹角求解;
解法三:以M为原点,MB,MC分别为x轴,y轴建立空间直角坐标系.计算出平面CDE的法向量和平面CEM的法向量,利用向量夹角求解;
(3)求出三棱锥D-CME的底面面积和高,代入体积公式,求解.
(2)解法一:连接DM,可证得DM⊥平面CME,过M作MF⊥CE交CE于点F,连接DF,则∠DFM即为二面角D-CE-M的平面角,解三角形求出答案;
解法二:以C为原点,CA,CB分别为x轴,y轴建立空间直角坐标系.计算出平面CDE的法向量和平面CEM的法向量,利用向量夹角求解;
解法三:以M为原点,MB,MC分别为x轴,y轴建立空间直角坐标系.计算出平面CDE的法向量和平面CEM的法向量,利用向量夹角求解;
(3)求出三棱锥D-CME的底面面积和高,代入体积公式,求解.
解答:
证明:(1)∵AC=2AE=2,CE=
,
∴AE2+AC2=CE2,即AE⊥AC;
又AE⊥AB,AB∩AC=C;
∴AE⊥平面ABC;
∵AE?平面ABDE;
∴平面ABDE⊥平面ABC…(4分)
(2)解法一:连接DM,可证得DM⊥平面CME,
过M作MF⊥CE交CE于点F,连接DF,
则∠DFM即为二面角D-CE-M的平面角.

计算得:DM=
,MF=
,DF=
.∴cos∠DFM=
=
…(9分)
解法二:以C为原点,CA,CB分别为x轴,y轴建立空间直角坐标系.
计算得,平面CDE的法向量
=(1,2,-2);
平面CEM的法向量
=(1,-1,-2).cos<
,
>=…=
,
所以,二面角D-CE-M的余弦值为
.
解法三:以M为原点,MB,MC分别为x轴,y轴建立空间直角坐标系.
计算得,平面CDE的法向量
=(-1,3,2
);
平面CEM的法向量
=(1,0,
).
cos<
,
>=
所以,二面角D-CE-M的余弦值为
.
(3)VD-CME=
•S△CME•MD=
•
•MC•ME•MD=
•
•
•
=1…(14分)
| 5 |
∴AE2+AC2=CE2,即AE⊥AC;
又AE⊥AB,AB∩AC=C;
∴AE⊥平面ABC;
∵AE?平面ABDE;
∴平面ABDE⊥平面ABC…(4分)
(2)解法一:连接DM,可证得DM⊥平面CME,
过M作MF⊥CE交CE于点F,连接DF,
则∠DFM即为二面角D-CE-M的平面角.

计算得:DM=
| 6 |
|
| 6 | ||
|
| MF |
| DF |
| ||
| 6 |
解法二:以C为原点,CA,CB分别为x轴,y轴建立空间直角坐标系.
计算得,平面CDE的法向量
| m |
平面CEM的法向量
| n |
| m |
| n |
| ||
| 6 |
所以,二面角D-CE-M的余弦值为
| ||
| 6 |
解法三:以M为原点,MB,MC分别为x轴,y轴建立空间直角坐标系.
计算得,平面CDE的法向量
| m |
| 2 |
平面CEM的法向量
| n |
| 2 |
cos<
| m |
| n |
| ||
| 6 |
所以,二面角D-CE-M的余弦值为
| ||
| 6 |
(3)VD-CME=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 6 |
点评:本题主要考查空间中的基本关系,考查线面垂直、面面垂直的判定以及线面角和几何体体积的计算,考查识图能力、空间想象能力和逻辑推理能力.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
若{x}表示“不小于x的最小整数”(如{1,2}=2),则当-3≤x≤3时,方程{x-1}=x的实数解有( )
| A、0个 | B、5个 | C、6个 | D、7个 |
抛物线y=x2上的点到直线x-y-2=0的最短距离为( )
A、
| ||||
B、
| ||||
C、2
| ||||
| D、1 |
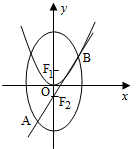 如图所示,椭圆C:
如图所示,椭圆C: