题目内容
16．对于函数f（x）定义域中任意的x1，x2（x1≠x2），有如下结论：①f（x1+x2）=f（x1）•f（x2）；
②f（x1•x2）=f（x1）•f（x2）；
③f（$\frac{{x}_{1}{+x}_{2}}{2}$）＞$\frac{f{（x}_{1}）+f{（x}_{2}）}{2}$；
④$\frac{f{（x}_{1}）-f{（x}_{2}）}{{x}_{1}{-x}_{2}}$＞0；
⑤当1＜x1＜x2时$\frac{f{（x}_{1}）}{{x}_{1}-1}＞\frac{f{（x}_{2}）}{{x}_{2}-1}$；
当f（x）=${（\frac{3}{2}）}^{x}$时，上述结论中正确结论的序号是①④⑤．
分析 利用函数的性质验证命题的真假即可．
解答 解：当f（x）=${（\frac{3}{2}）}^{x}$时，
①f（x1+x2）=$（\frac{3}{2}）^{{x}_{1}+{x}_{2}}$=$（\frac{3}{2}）^{{x}_{1}}•（\frac{3}{2}）^{{x}_{2}}$=f（x1）•f（x2），①正确；
②f（x1•x2）=$（\frac{3}{2}）^{{x}_{1}{x}_{2}}$≠f（x1）+f（x2），不正确；
③f（$\frac{{x}_{1}{+x}_{2}}{2}$）＞$\frac{f{（x}_{1}）+f{（x}_{2}）}{2}$，说明函数是凸函数，而f（x）=${（\frac{3}{2}）}^{x}$是凹函数，所以不正确；
④$\frac{f{（x}_{1}）-f{（x}_{2}）}{{x}_{1}{-x}_{2}}$＞0，说明函数是增函数，而f（x）=${（\frac{3}{2}）}^{x}$是增函数，所以正确；
⑤当1＜x1＜x2时$\frac{f{（x}_{1}）}{{x}_{1}-1}＞\frac{f{（x}_{2}）}{{x}_{2}-1}$．说明函数与（1，0）连线的斜率在减少，所以正确；
故答案为①④⑤．
点评 本题考查函数的基本性质的应用，考查命题的真假的判断，是基础题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7．已知函数y=f（x）和y=g（x）在[-2，2]上的图象如图所示，给出下列四个选项同，其中不正确的是（ ）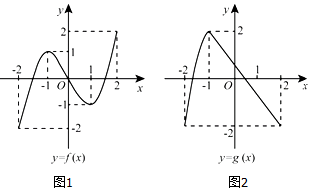
| A． | 函数f[g（x）]的零点有且仅有6个 | B． | 函数g[f（x）]的零点有且仅有3个 | ||
| C． | 函数f[f（x）]的零点有且仅有5个 | D． | 函数g[g（x）]的零点有且仅有4个 |
