题目内容
11.一幅广告印刷品的画面(矩形,如图①阴影部分)面积6m2,它的两边都留有宽为0.15m的空白,顶部和底部都留有宽为0.1m的空白(1)如何选择纸张的尺寸,才能使纸张的用量最少?
(2)如图②,将此广告张贴在墙上,其画面(不包含空白)的最高点A处离地面4m,最低点B处离地面2m,若从地面1.5m的C处观赏它,则离墙多远是,视角θ最大?

分析 (1)设纸张的长和宽,表示出纸张的面积,利用基本不等式求最值,即可得到结论.
(2)过C作CD⊥AB,垂足为D,设CD=xm,则θ=∠ACD-∠BCD,利用差角的正切公式,我们可以求得tanθ=$\frac{2}{x+\frac{\frac{5}{4}}{x}}$,利用基本不等式可得结论.
解答 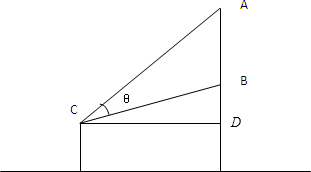 解:(1)设纸张的长和宽分别是x,y,则xy=6
解:(1)设纸张的长和宽分别是x,y,则xy=6
纸张的面积为:S=(y+0.2(x+0.3)
=xy+0.2x+0.3y+0.06≥xy+2$\sqrt{0.06xy}$+0.06
当且仅当0.2x=0.3y,即x=2,y=3时,
S有最小值6+$\sqrt{0.06}$,
此时纸张的长和宽分别为2m,3m;
(2)由题意,过C作CD⊥AB,垂足为D,
设CD=xm,则θ=∠ACD-∠BCD
∴tanθ=tan(∠ACD-∠BCD)=$\frac{\frac{2.5}{x}-\frac{0.5}{x}}{1+\frac{2.5}{x}×\frac{0.5}{x}}$=$\frac{2}{x+\frac{\frac{5}{4}}{x}}$,
∵x>0,∴tanθ≤$\frac{2\sqrt{5}}{5}$
∵$θ∈(0,\frac{π}{2})$.
∴当且仅当x=$\frac{\frac{5}{4}}{x}$,即x=$\frac{\sqrt{5}}{2}$m时,tanθ最大,即视角最大,
∴离墙$\frac{\sqrt{5}}{2}$m时tanθ最大,此时视角最大.
点评 本题考查函数模型的构建,考查差角的正切函数公式,考查利用基本不等式求最值,解题的关键是利用差角的正切函数公式构建函数模型.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
1.若sinαcos(α-β)-cosαsin(α-β)=m,且β为钝角,则cosβ的值为( )
| A. | $±\sqrt{1-{m^2}}$ | B. | $\sqrt{1-{m^2}}$ | C. | $±\sqrt{{m^2}-1}$ | D. | $-\sqrt{1-{m^2}}$ |
2.今有一组实验数据,如表:
现准备从以下函数中选择一个最能代表两个变量x、y之间的规律,则拟合最好的是( )
| x | 1.993 | 3.002 | 4.001 | 5.032 | 6.121 |
| y | 1.501 | 4.413 | 7.498 | 12.04 | 17.93 |
| A. | y=2x-1+1 | B. | $y=\frac{3}{2}{log_2}x$ | C. | $y=\frac{1}{2}{x^2}-\frac{1}{2}$ | D. | y=-2x-2 |
19.已知集合A={x|1<x≤3},B={x|x<4,x∈Z},则A∩B=( )
| A. | (2,3) | B. | [2,3] | C. | {2,3} | D. | {2,3,4} |
6.已知命题甲:a+b≠4,命题乙:a≠1且b≠3,则命题甲是命题乙的( )
| A. | 充分必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分不必要条件 | D. | 必要不充分条件 |
3.若△PAD所在平面与矩形ABCD所在平面互相垂直,PA=PD=AB=2,∠APD=60°,若点P,A,B,C,D都在同一个球面上,则此球的表面积为( )
| A. | $\frac{25}{3}$π | B. | $\frac{28}{3}$π | C. | $\frac{28\sqrt{21}}{27}$π | D. | $\frac{25\sqrt{21}}{27}$π |
 如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.
如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.