题目内容
8.已知等比数列{an}中a1=$\frac{27}{16}$,an=$\frac{1}{3}$,q=-$\frac{2}{3}$,则n=5.分析 根据题意,由等比数列{an}的a1与q的值,可得其通项公式,又由an=$\frac{1}{3}$,则有$\frac{27}{16}$×(-$\frac{2}{3}$)n-1=$\frac{1}{3}$,解可得n的值,即可得答案.
解答 解:根据题意,等比数列{an}中a1=$\frac{27}{16}$,q=-$\frac{2}{3}$,
则通项公式为an=a1×qn-1=$\frac{27}{16}$×(-$\frac{2}{3}$)n-1,
若an=$\frac{1}{3}$,则有$\frac{27}{16}$×(-$\frac{2}{3}$)n-1=$\frac{1}{3}$,
解可得n=5;
故答案为:5.
点评 本题考查等比数列的通项,注意牢记公式的形式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.己知α是第三象限角,且tanα=$\frac{5}{12}$,则cosα的值是( )
| A. | -$\frac{5}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
3.如图,直线l经过第二、第三、第四象限,l的倾斜角为α,斜率为k,则( )


| A. | ksin(π+α)>0 | B. | kcos(π-α)>0 | C. | ksinα≤0 | D. | kcosα≤0 |
2.已知函数f(x)=$\left\{\begin{array}{l}{|lgx|,0<x≤3}\\{f(6-x),3<x<6}\end{array}\right.$,设方程f(x)=2-x+b(b∈R)的四个实根从小到大依次为x1,x2,x3,x4,对于满足条件的任意一组实根,下列判断中一定正确的为( )
| A. | x1+x2=2 | B. | 9<x3•x4<25 | C. | 0<(6-x3)•(6-x4)<1 | D. | 1<x1•x2<9 |
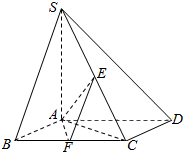 如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.
如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.