题目内容
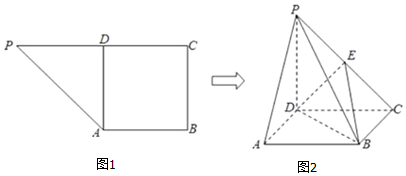
1．一个三角形可分为以内切圆半径为高，以原三角形三条边为底的三个三角形，类比此方法，若一个三棱锥的体积V=2，表面积S=3，则该三棱锥内切球的体积为（ ）| A． | 81π | B． | 16π | C． | $\frac{32π}{3}$ | D． | $\frac{16π}{9}$ |
分析 根据类似推理可以得到一个三棱锥分为以内切球半径为高，以原三角锥四个面为底的四个三角锥，利用等体积求出内切球半径，即可求出该三棱锥内切球的体积．
解答 解：由一个三角形可分为以内切圆半径为高，以原三角形三条边为底的三个三角形，
可以类比一个三棱锥分为以内切球半径为高，以原三角锥四个面为底的四个三角锥，
设三棱锥的四个面积分别为：S1，S2，S3，S4，
由于内切球到各面的距离等于内切球的半径
∴V=$\frac{1}{3}$（S1×r+S2×r+S3×r+S4×r）=$\frac{1}{3}$S×r
∴内切球半径r=$\frac{3V}{S}$=$\frac{2×3}{3}$=2，
∴该三棱锥内切球的体积为$\frac{4}{3}$π•23=$\frac{32π}{3}$．
故选：C
点评 本题考查类比推理的问题，以及三棱锥内切球的体积，考查学生的计算能力，求出内切球半径是关键．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
12．若复数z满足（1+i）z=2+i，则复数z的共轭复数$\overline z$在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
16．从标有数字1，2，3的三个红球和标有数字2，3的两个白球中任取两个球，则取得两球的数字和颜色都不相同的概率为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
13．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，（$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{a}$=7，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
10．已知i为虚数单位，复数z满足（1+i）z=（1-i）2，则|z|为（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
