题目内容
6．已知$tan（α+β）=\frac{1}{2}，tan（α+\frac{π}{4}）=-\frac{1}{3}$，则$tan（β-\frac{π}{4}）$=（ ）| A． | 2 | B． | $\frac{3}{2}$ | C． | 1 | D． | $\frac{1}{2}$ |
分析 由已知利用两角差的正切函数公式即可计算得解．
解答 解：∵$tan（α+β）=\frac{1}{2}，tan（α+\frac{π}{4}）=-\frac{1}{3}$，
∴$tan（β-\frac{π}{4}）$=tan[（α+β）-（α+$\frac{π}{4}$）]=$\frac{tan（α+β）-tan（α+\frac{π}{4}）}{1+tan（α+β）tan（α+\frac{π}{4}）}$=$\frac{\frac{1}{2}-（-\frac{1}{3}）}{1+\frac{1}{2}×（-\frac{1}{3}）}$=1．
故选：C．
点评 本题主要考查了两角差的正切函数公式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
17．某品牌电脑专卖店的年销售量y与该年广告费用x有关，如表收集了4组观测数据：
以广告费用x为解释变量，销售量y为预报变量对这两个变量进行统计分析．
（1）已知这两个变量呈线性相关关系，试建立y与x之间的回归方程$\hat y=\hat bx+\hat a$；
（2）假如2017年该专卖店广告费用支出计划为10万元，请根据你得到的模型，预测这一年的销售量y．
参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
| x（万元） | 1 | 4 | 5 | 6 |
| y（百台） | 30 | 40 | 60 | 50 |
（1）已知这两个变量呈线性相关关系，试建立y与x之间的回归方程$\hat y=\hat bx+\hat a$；
（2）假如2017年该专卖店广告费用支出计划为10万元，请根据你得到的模型，预测这一年的销售量y．
参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
14．
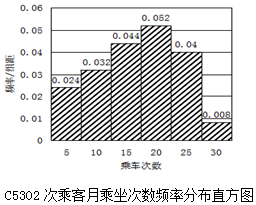孝汉城铁于12月1日开通，C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况，分别在两个车次各随机抽取了100名旅客进行调查，下面是根据调查结果，绘制了乘车次数的频率分布直方图和频数分布表．
C5321次乘客月乘坐次数频数分布表
（1）若将频率视为概率，月乘车次数不低于15次的称之为“老乘客”，试问：哪一车次的“老乘客”较多，简要说明理由．
（2）已知在C5321次列车随机抽到的50岁以上人员有35名，其中有10名是“老乘客”，由条件完成下面2×2列联表，并根据资料判断，是否有90%的把握认为年龄有乘车次数有关，说明理由．
附：随机变量${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d为样本总量）
孝汉城铁于12月1日开通，C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况，分别在两个车次各随机抽取了100名旅客进行调查，下面是根据调查结果，绘制了乘车次数的频率分布直方图和频数分布表．C5321次乘客月乘坐次数频数分布表
| 乘车次数分组 | 频数 |
| [0，5） | 15 |
| [5，10） | 20 |
| [10，15） | 25 |
| [15，20） | 24 |
| [20，25） | 11 |
| [25，30] | 5 |
（2）已知在C5321次列车随机抽到的50岁以上人员有35名，其中有10名是“老乘客”，由条件完成下面2×2列联表，并根据资料判断，是否有90%的把握认为年龄有乘车次数有关，说明理由．
| 老乘客 | 新乘客 | 合计 | |
| 50岁以上 | 10 | 25 | 35 |
| 50岁以下 | 30 | 35 | 65 |
| 合计 | 40 | 60 | 100 |
| P（k2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
11．已知A={x|y2=x}，B={y|y2=x}，则（ ）
| A． | A∪B=A | B． | A∩B=A | C． | A=B | D． | （∁RA）∩B=∅ |
15．已知函数f（x）=$\sqrt{1-x}$+$\sqrt{x+3}$的最大值为M，最小值为m，则$\frac{m}{M}$的值为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{5}}{3}$ |