题目内容
9．设等差数列{an}{bn}前项和为Sn、Tn，若对任意的n∈N*，都有$\frac{S_n}{T_n}=\frac{2n-3}{4n-3}$，则$\frac{a_2}{{{b_3}+{b_{13}}}}+\frac{{{a_{14}}}}{{{b_5}+{b_{11}}}}$的值为（ ）| A． | $\frac{29}{45}$ | B． | $\frac{13}{29}$ | C． | $\frac{9}{19}$ | D． | $\frac{19}{30}$ |
分析 由等差数列的性质和求和公式可得原式=$\frac{{S}_{15}}{{T}_{15}}$，代值计算可得．
解答 解：由等差数列的性质和求和公式可得：$\frac{a_2}{{{b_3}+{b_{13}}}}+\frac{{{a_{14}}}}{{{b_5}+{b_{11}}}}$=$\frac{{2a}_{8}}{{2b}_{8}}$=$\frac{\frac{15}{2}（{a}_{1}+{a}_{15}）}{\frac{15}{2}（{b}_{1}+{b}_{15}）}$=$\frac{{S}_{15}}{{T}_{15}}$=$\frac{27}{57}$=$\frac{9}{19}$．
故选C．
点评 本题考查等差数列的性质和求和公式，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
20．
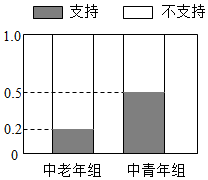国家实施二孩放开政策后，为了了解人们对此政策持支持态度是否与年龄有关，计生部门将已婚且育有一孩的居民分成中老年组（45岁以上，含45岁）和中青年组（45岁以下，不含45岁）两个组别，每组各随机调查了50人，对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图，如图所示：
（1）根据以上信息完成2×2列联表；
（2）是否有99%以上的把握认为人们对此政策持支持态度与年龄有关？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
国家实施二孩放开政策后，为了了解人们对此政策持支持态度是否与年龄有关，计生部门将已婚且育有一孩的居民分成中老年组（45岁以上，含45岁）和中青年组（45岁以下，不含45岁）两个组别，每组各随机调查了50人，对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图，如图所示：| 支持 | 不支持 | 合计 | |
| 中老年组 | 10 | 40 | 50 |
| 中青年组 | 25 | 25 | 50 |
| 合 计 | 35 | 65 | 100 |
（2）是否有99%以上的把握认为人们对此政策持支持态度与年龄有关？
| P（K2≥k0） | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
17．某品牌电脑专卖店的年销售量y与该年广告费用x有关，如表收集了4组观测数据：
以广告费用x为解释变量，销售量y为预报变量对这两个变量进行统计分析．
（1）已知这两个变量呈线性相关关系，试建立y与x之间的回归方程$\hat y=\hat bx+\hat a$；
（2）假如2017年该专卖店广告费用支出计划为10万元，请根据你得到的模型，预测这一年的销售量y．
参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
| x（万元） | 1 | 4 | 5 | 6 |
| y（百台） | 30 | 40 | 60 | 50 |
（1）已知这两个变量呈线性相关关系，试建立y与x之间的回归方程$\hat y=\hat bx+\hat a$；
（2）假如2017年该专卖店广告费用支出计划为10万元，请根据你得到的模型，预测这一年的销售量y．
参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
4．已知集合M={y|y=-x2+4}，N={x|y=log2x}，则M∩N=（ ）
| A． | [4，+∞） | B． | （-∞，4] | C． | （0，4） | D． | （0，4] |
14．
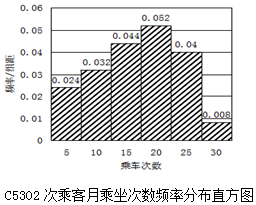孝汉城铁于12月1日开通，C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况，分别在两个车次各随机抽取了100名旅客进行调查，下面是根据调查结果，绘制了乘车次数的频率分布直方图和频数分布表．
C5321次乘客月乘坐次数频数分布表
（1）若将频率视为概率，月乘车次数不低于15次的称之为“老乘客”，试问：哪一车次的“老乘客”较多，简要说明理由．
（2）已知在C5321次列车随机抽到的50岁以上人员有35名，其中有10名是“老乘客”，由条件完成下面2×2列联表，并根据资料判断，是否有90%的把握认为年龄有乘车次数有关，说明理由．
附：随机变量${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d为样本总量）
孝汉城铁于12月1日开通，C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况，分别在两个车次各随机抽取了100名旅客进行调查，下面是根据调查结果，绘制了乘车次数的频率分布直方图和频数分布表．C5321次乘客月乘坐次数频数分布表
| 乘车次数分组 | 频数 |
| [0，5） | 15 |
| [5，10） | 20 |
| [10，15） | 25 |
| [15，20） | 24 |
| [20，25） | 11 |
| [25，30] | 5 |
（2）已知在C5321次列车随机抽到的50岁以上人员有35名，其中有10名是“老乘客”，由条件完成下面2×2列联表，并根据资料判断，是否有90%的把握认为年龄有乘车次数有关，说明理由．
| 老乘客 | 新乘客 | 合计 | |
| 50岁以上 | 10 | 25 | 35 |
| 50岁以下 | 30 | 35 | 65 |
| 合计 | 40 | 60 | 100 |
| P（k2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
2．已知函数f（x）=$\left\{\begin{array}{l}{（a+1）x-2a，x＜3}\\{lo{g}_{3}x，x≥3}\end{array}\right.$的值域为R，则实数a的范围是（ ）
| A． | [-1，1] | B． | （-1，1] | C． | （-1，+∞） | D． | （-∞，-1） |