题目内容
4.为得到函数y=sin2x-cos2x的图象,可由函数y=$\sqrt{2}$sin2x的图象( )| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向右平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
分析 由条件利用两角差的正弦公式,函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:∵函数y=sin2x-cos2x=$\sqrt{2}$sin(2x-$\frac{π}{4}$)=$\sqrt{2}$sin[2(x-$\frac{π}{8}$)],
∴把函数y=$\sqrt{2}$sin2x的图象向右平移$\frac{π}{8}$个单位,可得函数y=sin2x-cos2x的图象,
故选:B.
点评 本题主要考查两角差的正弦公式,函数y=Asin(ωx+φ)的图象变换规律的简单应用,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
14.已知函数$f(x)=sin(\frac{π}{3}x+φ)(|φ|<\frac{π}{2})$的图象关于直线x=1对称,把f(x)的图象向右平移3个单位长度后,所得图象对应的函数解析式为( )
| A. | y=sin($\frac{π}{3}$x+$\frac{π}{6}$) | B. | y=sin($\frac{π}{3}$x-$\frac{π}{6}$) | C. | y=cos($\frac{π}{3}$x+$\frac{π}{6}$) | D. | y=sin($\frac{π}{3}$x-$\frac{5π}{6}$) |
9.已知变量x与y负相关,且由观测数据计算得样本平均数$\overline x=4,\overline y=6.5$,则由该观测数据算得的线性回归方程可能是( )
| A. | y=2x-1.5 | B. | y=0.8x+3.3 | C. | y=-2x+14.5 | D. | y=-0.6x+9.1 |
14.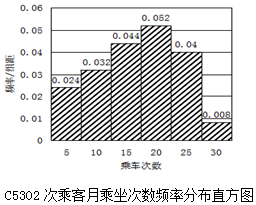 孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.
孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.
C5321次乘客月乘坐次数频数分布表
(1)若将频率视为概率,月乘车次数不低于15次的称之为“老乘客”,试问:哪一车次的“老乘客”较多,简要说明理由.
(2)已知在C5321次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成下面2×2列联表,并根据资料判断,是否有90%的把握认为年龄有乘车次数有关,说明理由.
附:随机变量${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d为样本总量)
 孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.
孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.C5321次乘客月乘坐次数频数分布表
| 乘车次数分组 | 频数 |
| [0,5) | 15 |
| [5,10) | 20 |
| [10,15) | 25 |
| [15,20) | 24 |
| [20,25) | 11 |
| [25,30] | 5 |
(2)已知在C5321次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成下面2×2列联表,并根据资料判断,是否有90%的把握认为年龄有乘车次数有关,说明理由.
| 老乘客 | 新乘客 | 合计 | |
| 50岁以上 | 10 | 25 | 35 |
| 50岁以下 | 30 | 35 | 65 |
| 合计 | 40 | 60 | 100 |
| P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
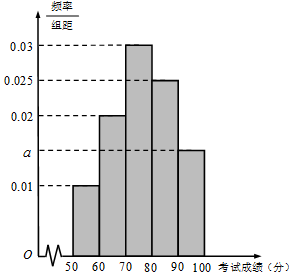 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.