题目内容
9.向量$\overrightarrow{a}$=(1,-2)与$\overrightarrow{b}$=(3,t)的夹角为θ,$\overrightarrow{c}$=(1,-3),$\overrightarrow{b}$⊥$\overrightarrow{c}$,则cosθ=$\frac{\sqrt{2}}{10}$.分析 根据向量的数量积的运算和向量的夹角公式计算即可.
解答 解:∵$\overrightarrow{a}$=(1,-2)与$\overrightarrow{b}$=(3,t)的夹角为θ,$\overrightarrow{c}$=(1,-3),$\overrightarrow{b}$⊥$\overrightarrow{c}$,
∴3×1-3t=0,
∴t=1,
∴$\overrightarrow{b}$=(3,1),
∴|$\overrightarrow{a}$|=$\sqrt{5}$,|$\overrightarrow{b}$|=$\sqrt{10}$,$\overrightarrow{a}$•$\overrightarrow{b}$=1×3-2×1=1,
∴cosθ=$\frac{1}{\sqrt{5}•\sqrt{10}}$=$\frac{\sqrt{2}}{10}$
故答案为:$\frac{\sqrt{2}}{10}$.
点评 本题考查数量积表示向量的夹角,以及向量的数量积的运算,属于基础题.

练习册系列答案
相关题目
4.阅读如图所示的程序框图,运行相应的程序,若判断框内是n≤6,则输出的S为( )
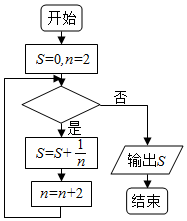

| A. | $\frac{3}{4}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{5}{6}$ |
14.设命题p:?x∈(0,+∞),$\sqrt{x}$≥log2x,则¬p为( )
| A. | ?x∈(0,+∞),$\sqrt{x}$≥log2x | B. | ?x∈(0,+∞),$\sqrt{x}$<log2x | C. | ?x∈(0,+∞),$\sqrt{x}$=log2x | D. | ?x∈(0,+∞),$\sqrt{x}$<log2x |
1.某几何体的三视图如图所示,则该几何体的体积为( )
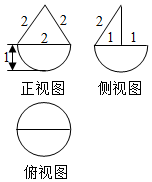

| A. | $\frac{4+\sqrt{3}}{3}$π | B. | $\frac{4+\sqrt{3}}{6}$π | C. | $\frac{2+\sqrt{3}}{3}$π | D. | $\frac{5π}{6}$ |
19.函数f(x)=sin2x和函数g(x)的部分图象如图所示,则函数g(x)的解析式可以是( )

| A. | g(x)=sin(2x-$\frac{π}{3}}$) | B. | g(x)=sin(2x+$\frac{2π}{3}}$) | C. | g(x)=cos(2x+$\frac{5π}{6}}$) | D. | g(x)=cos(2x-$\frac{π}{6}}$) |
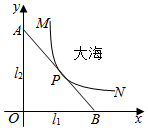 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,点P到l2的距离为2千米.以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,点P到l2的距离为2千米.以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy.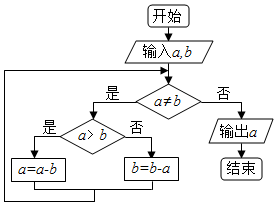 上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )
上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )