题目内容
1.某几何体的三视图如图所示,则该几何体的体积为( )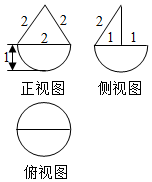
| A. | $\frac{4+\sqrt{3}}{3}$π | B. | $\frac{4+\sqrt{3}}{6}$π | C. | $\frac{2+\sqrt{3}}{3}$π | D. | $\frac{5π}{6}$ |
分析 几何体为半球与半圆锥的组合体.
解答 解:由三视图可知几何体为半球与半圆锥的组合体.
半球的半径为1,半圆锥的底面半径为1,母线为2,故圆锥的高为$\sqrt{3}$.
∴圆锥的体积V=$\frac{1}{2}×\frac{4}{3}π×{1}^{3}$+$\frac{1}{2}×\frac{1}{3}π×{1}^{2}×\sqrt{3}$=$\frac{4+\sqrt{3}}{6}π$.
故选B.
点评 本题考查了圆锥与球的三视图,结构特征和体积计算,属于基础题.

练习册系列答案
相关题目
12.函数f(x)=cosx•log2|x|的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
16.若函数f(x)=$\left\{\begin{array}{l}{lnx,(x>0)}\\{{e}^{x+1}-2,(x≤0)}\end{array}\right.$,则f(f($\frac{1}{e}$))=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 3 |
13.已知i是虚数单位,则复数z=$\frac{1+2i}{3-4i}$的虚部是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | -$\frac{1}{5}$ | D. | $\frac{2}{5}$i |
11.执行如图所示的程序框图,输出的i为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
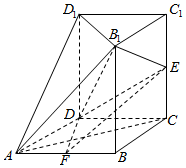 如图,几何体ABCD-B1C1D1中,四边形ABCD为菱形,∠BAD=60°,AB=a,平面B1C1D1∥平面ABCD,BB1、CC1、DD1都垂直于平面ABCD,且BB1=$\sqrt{2}$a,E为CC1的中点,F为AB的中点.
如图,几何体ABCD-B1C1D1中,四边形ABCD为菱形,∠BAD=60°,AB=a,平面B1C1D1∥平面ABCD,BB1、CC1、DD1都垂直于平面ABCD,且BB1=$\sqrt{2}$a,E为CC1的中点,F为AB的中点.