题目内容

命题“?x∈R，e＞x”的否定是（　　）
A、?x∈R，ex＜x
B、?x∈R，ex＜x
C、?x∈R，ex≤x
D、?x∈R，ex≤x
考点：命题的否定
专题：简易逻辑
分析：直接利用全称命题是否定是特称命题写出结果即可．
解答： 解：因为全称命题的否定是特称命题，所以，命题“?x∈R，e＞x”的否定是：?x∈R，ex≤x．
故选：D．
点评：本题考查命题的否定特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
相关题目
使函数y=2tanx与y=cosx同时单调递增的区间为
 
．
已知|
a
|=12，|
b
|=9，
a
•
b
=54
2
，则
a
与
b
的夹角为
 
．
cos
65
6
π=（　　）
A、
1
2
B、-
1
2
C、-
3
2
D、
3
2
已知向量
a
=（1，2），
b
=（-2，k），且
a
∥
b
，则实数k=
 
．
命题“?x∈R，x2-x+1≤0”的否定是
 
．
已知i是虚数单位，且（x-i）（1-i）=y，则实数x，y分别为（　　）
A、x=-1，y=1
B、x=-1，y=2
C、x=1，y=1
D、x=-1，y=-2
已知集体A={x||x|＜3}，B={x|y=
x-1
}，则集合A∩B=
 
．
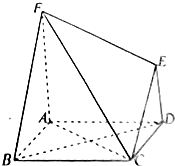在如图所示的多面体ABCDEF中，四边形ABCD是正方形，AF⊥平面ABCD，DE⊥平面ABCD，且AF=2DE
（Ⅰ）求证：BD∥平面CEF．
（Ⅱ）若异面直线AB和CE成角为45°，求二面角B-CF-A的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网