题目内容
已知|
|=12，|
|=9，
•
=54
，则
与
的夹角为 ．
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：由向量的夹角公式可得cosθ=
，代值计算由特殊角的三角函数可得．
| ||||
|
|
解答：
解：设
与
的夹角为θ，
则cosθ=
=
=
，
∵θ∈[0，π]，∴θ=
故答案为：
| a |
| b |
则cosθ=
| ||||
|
|
54
| ||
| 12×9 |
| ||
| 2 |
∵θ∈[0，π]，∴θ=
| π |
| 4 |
故答案为：
| π |
| 4 |
点评：本题考查向量的夹角公式，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
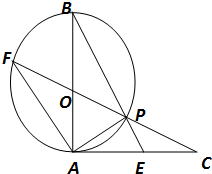已知：如图，AB是⊙O的直径，AC与⊙O相切于点A，且AC=AB，CO与⊙O相交于点P，CO的延长线与⊙O相交于点F，BP的延长线与AC相交于点E．已知f（x）=
，则f（
）的值是（ ）
|
| ||
| 2 |
| A、0 | ||
| B、1 | ||
C、
| ||
D、-
|
命题“?x∈R，e＞x”的否定是（ ）
| A、?x∈R，ex＜x |
| B、?x∈R，ex＜x |
| C、?x∈R，ex≤x |
| D、?x∈R，ex≤x |
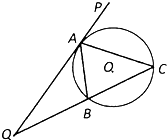如图，直线 PQ与⊙O相切于点 A，A B是⊙O的弦，∠P A B的平分线 AC交⊙O于点C，连结C B，并延长与直线 PQ相交于点Q．