题目内容
设复数z满足|
-3-3i|-2|z|=0(i是虚数单位),则|z|的最小值为 .
. |
| z |
考点:复数求模
专题:数系的扩充和复数
分析:设出复数z的代数形式,得到
,代入|
-3-3i|-2|z|=0整理得到(a+1)2+(b-1)2=8.由此可得复数z对应的点Z的轨迹为以(-1,1)为圆心,以2
为半径的圆.数形结合求得|z|的最小值.
. |
| z |
. |
| z |
| 2 |
解答:
解:设z=a+bi(a,b∈R),则
=a-bi,
代入|
-3-3i|-2|z|=0,得:
|a-bi-3-3i|-2|a+bi|=0,即|(a-3)-(b+3)i|-2|a+bi|=0,
∴
=2
,
整理得:(a+1)2+(b-1)2=8.
∴复数z对应的点的轨迹为以(-1,1)为圆心,以2
为半径的圆.
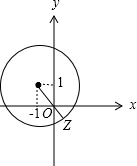
∴|z|的最小值为2
-
=
.
故答案为:
.
. |
| z |
代入|
. |
| z |
|a-bi-3-3i|-2|a+bi|=0,即|(a-3)-(b+3)i|-2|a+bi|=0,
∴
| (a-3)2+(b+3)2 |
| a2+b2 |
整理得:(a+1)2+(b-1)2=8.
∴复数z对应的点的轨迹为以(-1,1)为圆心,以2
| 2 |

∴|z|的最小值为2
| 2 |
| 2 |
| 2 |
故答案为:
| 2 |
点评:本题考查复数模的求法,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
椭圆的长轴为6,短轴为4,则椭圆的标准方程是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、以上都不是 |