题目内容
11.已知定义在R上的偶函数f(x),满足f(x)=-f(4-x),且当x∈[2,4)时,f(x)=log2(x-1),则f(19)的值为( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 推导出函数的周期是8.再由当x∈[2,4)时,f(x)=log2(x-1),能求出f(19).
解答 解:∵定义在R上的偶函数f(x),满足f(x)=-f(4-x),
∴由题意定义在R上的偶函数f(x),满足f(x)=-f(4-x),
得f(x)=-f(x-4),此式恒成立,故可得f(x)=f(x-8),
由此式恒成立可得,此函数的周期是8.
又当x∈[2,4)时,f(x)=log2(x-1),
∴f(19)=f(3)=log2(3-1)=1.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
19.若a=log${\;}_{\frac{1}{2}}}$3,b=log3$\frac{1}{2}$,c=20.3,则( )
| A. | a<b<c | B. | b<a<c | C. | b<c<a | D. | a<c<b |
6.方程log2(x+2)=$\sqrt{-x}$的实数解的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
16.若不等式|x-2|+|x+3|>a恒成立,则a的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,5) | D. | (5,+∞) |
1.某几何体的三视图如图所示,该几何体的体积为( )


| A. | 24 | B. | $\frac{70}{3}$ | C. | 20 | D. | $\frac{68}{3}$ |
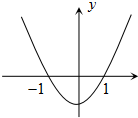 设f(x)=ax3+bx2+cx的极小值为-2,其导函数y=f′(x)的图象是经过点(-1,0),(1,0)开口向上的抛物线,如图所示.
设f(x)=ax3+bx2+cx的极小值为-2,其导函数y=f′(x)的图象是经过点(-1,0),(1,0)开口向上的抛物线,如图所示.