题目内容
(1)m为何值时,f(x)=x2+2mx+3m+4.有且仅有一个零点;
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:(1)根据一元二次函数和一元二次方程之间的关系,利用判别式△=0,即可得到结论.
(2)利用数形结合将函数零点问题转化为函数图象的交点个数问题即可得到结论.
(2)利用数形结合将函数零点问题转化为函数图象的交点个数问题即可得到结论.
解答:
 解:(1)f(x)=x2+2mx+3m+4有且仅有一个零点?方程f(x)=0有两个相等实根
解:(1)f(x)=x2+2mx+3m+4有且仅有一个零点?方程f(x)=0有两个相等实根
?△=0,
即4m2-4(3m+4)=0,
即m2-3m-4=0,∴m=4或m=-1.
(2)令f(x)=0,得|4x-x2|+a=0,
即|4x-x2|=-a.
令g(x)=|4x-x2|,h(x)=-a.
作出g(x)、h(x)的图象.
由图象可知,当0<-a<4,
即-4<a<0时,g(x)与h(x)的图象有4个交点,
即f(x)有4个零点.
故a的取值范围为(-4,0).
 解:(1)f(x)=x2+2mx+3m+4有且仅有一个零点?方程f(x)=0有两个相等实根
解:(1)f(x)=x2+2mx+3m+4有且仅有一个零点?方程f(x)=0有两个相等实根?△=0,
即4m2-4(3m+4)=0,
即m2-3m-4=0,∴m=4或m=-1.
(2)令f(x)=0,得|4x-x2|+a=0,
即|4x-x2|=-a.
令g(x)=|4x-x2|,h(x)=-a.
作出g(x)、h(x)的图象.
由图象可知,当0<-a<4,
即-4<a<0时,g(x)与h(x)的图象有4个交点,
即f(x)有4个零点.
故a的取值范围为(-4,0).
点评:本题主要考查函数零点的判断以及函数零点的应用,利用方程和函数之间的关系,结合数形结合是解决本题的关键.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
等边三角形ABC的边长为1,
=
,
=
,
=
,那么
•
+
•
+
•
等于( )
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
设
=2,则tan(α+
)=( )
| sinα+cosα |
| sinα-cosα |
| π |
| 4 |
| A、-2 | B、2 | C、-4 | D、4 |
要得到函数y=sinx的图象,只需将函数y=cos(x-
)+2的图象沿向量
平移得到,则
为( )
| π |
| 3 |
| a |
| a |
A、(-
| ||
B、(
| ||
C、(-
| ||
D、(
|
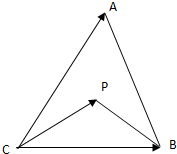 如图示,已知A、B、C为平面上的三个定点,∠ACB=60°,动点P在∠ACB的平分线上,记
如图示,已知A、B、C为平面上的三个定点,∠ACB=60°,动点P在∠ACB的平分线上,记