题目内容
设
=2,则tan(α+
)=( )
| sinα+cosα |
| sinα-cosα |
| π |
| 4 |
| A、-2 | B、2 | C、-4 | D、4 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:只需对分子分母同时除以cosθ,将原式转化成关于tanθ的表达式,最后利用两角和与差的正切函数求出结果即可.
解答:
解:∵
=2,
∴
=2,
∴tan(α+
)=
=-2
故选:A.
| sinα+cosα |
| sinα-cosα |
∴
| tanα+1 |
| tanα-1 |
∴tan(α+
| π |
| 4 |
| tanα+1 |
| 1-tanα |
故选:A.
点评:本题考查了齐次式的化简,利用条件和结论间的关系直接求解比较简单,属于中档题.

练习册系列答案
相关题目
若f′(x0)=-2,则
等于( )
| lim |
| k→0 |
f[x0-
| ||
| k |
| A、-1 | B、1 | C、-2 | D、2 |
如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论不成立的是( )
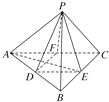

| A、BC∥平面PDF |
| B、DF⊥平面PAE |
| C、平面PDF⊥平面PAE |
| D、平面PDE⊥平面ABC |
复数(2+i)3的共轭复数对应的点,在复平面内位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若关于x的不等式|x-1|+|x+2|<a的解集为空集,则实数a的取值范围是( )
| A、(-∞,3) |
| B、(-∞,3] |
| C、[3,+∞) |
| D、(3,+∞) |
已知集合A={x|(
)x>
},B={x|log2(x-1)<2},则A∩B等于( )
| 1 |
| 2 |
| 1 |
| 4 |
| A、(-∞,5) |
| B、(-∞,2) |
| C、(1,2) |
| D、(2,5) |