题目内容
等边三角形ABC的边长为1，
=
，
=
，
=
，那么
•
+
•
+
•
等于（ ）
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积运算可得
•
=
•
=-
•
=-1×1×cos60°=-
．同理可得
•
=
•
=-
．即可得出．
| a |
| b |
| BC |
| CA |
| CB |
| CA |
| 1 |
| 2 |
| b |
| c |
| c |
| a |
| 1 |
| 2 |
解答：
解：∵
•
=
•
=-
•
=-1×1×cos60°=-
．
同理可得
•
=
•
=-
．
∴
•
+
•
+
•
=-
×3=-
．
故选：A．
| a |
| b |
| BC |
| CA |
| CB |
| CA |
| 1 |
| 2 |
同理可得
| b |
| c |
| c |
| a |
| 1 |
| 2 |
∴
| a |
| b |
| b |
| c |
| c |
| a |
| 1 |
| 2 |
| 3 |
| 2 |
故选：A．
点评：本题考查了数量积运算、等边三角形的性质，注意向量的夹角，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若f′（x0）=-2，则
等于（ ）
| lim |
| k→0 |
f[x0-
| ||
| k |
| A、-1 | B、1 | C、-2 | D、2 |
对于平面α和两直线m、n，下列表述正确的是（ ）
| A、m?α，n?α，则m，n相交 |
| B、若m∥α，m∥n，则n∥α |
| C、若m?α，n∥α，则m∥n |
| D、若m∥α，则m平行于α内的无数条直线 |
已知复数z=
，则z的共轭复数等于（ ）
| 1-i |
| 1+i |
| A、i | B、2i | C、-i | D、-2i |
某厂生产产品x件的总成本c（x）=1200+
x3（万元），已知产品单价P（万元）与产品件数x满足：P2=
，生产100件这样的产品单价为50万元，产量定为多少件时总利润最大？（ ）
| 2 |
| 75 |
| k |
| x |
| A、23 | B、24 | C、25 | D、26 |
如图，在正四面体P-ABC中，D、E、F分别是AB、BC、CA的中点，下面四个结论不成立的是（ ）
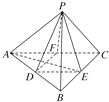
| A、BC∥平面PDF |
| B、DF⊥平面PAE |
| C、平面PDF⊥平面PAE |
| D、平面PDE⊥平面ABC |
复数（2+i）3的共轭复数对应的点，在复平面内位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |