题目内容
2.已知函数y=3sin($\frac{1}{2}$x-$\frac{π}{4}$)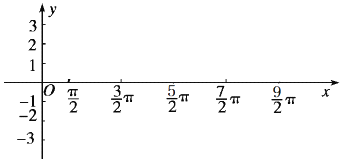
(1)求此函数的振幅、周期和初相;
(2)用五点法在给定的坐标系中作出函数一个周期的图象.(先列表再作图)
| $\frac{1}{2}$x-$\frac{π}{4}$ | |||||
| x | |||||
| 3sin($\frac{1}{2}$x-$\frac{π}{4}$) |
分析 (1)根据周期、振幅、初相的概念即可求出结果;(2)利用五点作图法即可做出图象
解答 解:(1)周期T=$\frac{2π}{ω}$=4π,(2分); 振幅A=3,初相是-$\frac{π}{4}$. (4分)
(2)列表:
| x | $\frac{π}{2}$ | $\frac{3}{2}π$ | $\frac{5}{2}π$ | $\frac{7}{2}π$ | $\frac{9}{2}π$ |
| $\frac{1}{2}$x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3}{2}π$ | 2π |
| 3sin($\frac{1}{2}$x-$\frac{π}{4}$) | 0 | 3 | 0 | -3 | 0 |
描点、连线,如图所示:
 (12分)
(12分)点评 本题主要考查三角函数的图象和性质,要求熟练掌握五点作图法,以及熟练掌握三角函数的有关概念和性质.

练习册系列答案
相关题目
10.已知函数$f(x)=sin({ωx+\frac{π}{4}})({ω>0})在({\frac{π}{2},π})$单调递减,则ω的取值范围可以是( )
| A. | $[{\frac{1}{2},\frac{5}{4}}]$ | B. | $[{0,\frac{5}{4}}]$ | C. | $({0,\frac{1}{2}}]$ | D. | (0,2] |
17.已知 sinα>0,cosα<0,则角α的终边在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
14.已知sin($\frac{π}{6}$-α)=$\frac{1}{3}$,则$cos[{2(\frac{π}{3}+α)}]$的值是( )
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |