题目内容
一个球的体积为4
π,则表面积为 .
| 3 |
考点:球的体积和表面积
专题:球
分析:利用球的体积求出球的半径,然后求解球的表面积.
解答:
解:设球的半径为r,由题意可得:
r3=4
π,解得r=
.
所以球的表面积为:4πr2=12π.
故答案为:12π.
| 4π |
| 3 |
| 3 |
| 3 |
所以球的表面积为:4πr2=12π.
故答案为:12π.
点评:本题考查球的体积以及表面积公式的应用,基本知识的考查.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
不等式(x-2)(4-x)>0的解集为( )
| A、{x|x<2} |
| B、{x|x>4} |
| C、{x|x<2或x>4} |
| D、{x|2<x<4} |
已知集合A={x|x2-4x<0},B={x|x-2>0},则A∩B=( )
| A、(0,2) |
| B、(0,4) |
| C、(4,+∞) |
| D、(2,4) |
复数z1=1+i,z2=3+ai,且3z1=z2,则a=( )
| A、0 | B、1 | C、2 | D、3 |
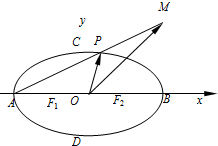 如图,在直角坐标系xOy中,椭圆
如图,在直角坐标系xOy中,椭圆 如图,已知圆G:x2-x+y2=0,经过抛物线y2=2px的焦点,过点(m,0)(m<0)倾斜角为
如图,已知圆G:x2-x+y2=0,经过抛物线y2=2px的焦点,过点(m,0)(m<0)倾斜角为