题目内容
14．已知a，b是常数，ab≠0，若函数f（x）=ax3+barcsinx+3的最大值为10，则f（x）的最小值为-4．分析 记函数g（x）=ax3+barcsinx，由函数的奇偶性和最值的关系可得．
解答 解：记函数g（x）=ax3+barcsinx，
∵g（-x）=-ax3-barcsinx=-g（x），∴函数g（x）为奇函数，
设当x=x0时，函数f（x）=ax3+barcsinx+3的最大值为10，
则f（x0）=ax03+barcsinx0+3=10，此时g（x）取最大值g（x0）=7，
由奇函数的性质可得当x=-x0时，函数g（x）取最小值g（-x0）=-7，
∴当x=-x0时，函数f（x）取最小值-7+3=-4，
故答案为：-4．
点评 本题考查三角函数的最值，涉及函数的奇偶性和最值，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
4．已知三棱锥P-ABC，在底面△ABC中，∠A=60°，$BC=\sqrt{3}$，PA⊥面ABC，PA=2，则此三棱锥的外接球的体积为（ ）
| A． | $\frac{{8\sqrt{2}}}{3}π$ | B． | $4\sqrt{3}π$ | C． | $\frac{{4\sqrt{2}π}}{3}$ | D． | 8π |
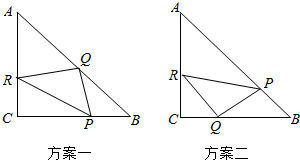在一个直角边长为10m的等腰直角三角形ABC的草地上，铺设一个也是等腰直角三角形PQR的花地，要求P，Q，R三点分别在△ABC的三条边上，且要使△PQR的面积最小，现有两种设计方案：
3．设命题p：?x＞1，x2+1＞2，则￢p为（ ）
| A． | ?x＞1，x2+1≤2 | B． | ?x＞1，x2+1≤2 | C． | ?x≤1，x2+1≤2 | D． | ?x≤1，x2+1≤2 |