题目内容
9.设向量$\overrightarrow{a}$=(3,3),$\overrightarrow{b}$=(1,-1),若($\overrightarrow{a}$+λ$\overrightarrow{b}$)⊥($\overrightarrow{a}$-λ$\overrightarrow{b}$),则实数λ=( )| A. | 3 | B. | 1 | C. | ±1 | D. | ±3 |
分析 根据向量垂直与向量坐标之间的关系建立方程关系,即可得到结论.
解答 解:向量$\overrightarrow{a}$=(3,3),$\overrightarrow{b}$=(1,-1),
∴$\overrightarrow{a}$+λ$\overrightarrow{b}$=(3+λ,3-λ),$\overrightarrow{a}$-λ$\overrightarrow{b}$=(3-λ,3+λ),
∵($\overrightarrow{a}$+λ$\overrightarrow{b}$)⊥($\overrightarrow{a}$-λ$\overrightarrow{b}$),
∴($\overrightarrow{a}$+λ$\overrightarrow{b}$)•($\overrightarrow{a}$-λ$\overrightarrow{b}$)=0,
∴(3+λ)(3-λ)+(3+λ)(3-λ)=0,
∴λ2=9,
∴λ=±3,
故选:D.
点评 本题主要考查向量垂直的坐标公式的应用,比较基础.

练习册系列答案
相关题目
19.下列命题中的假命题是( )
| A. | 若a<b<0,则$\frac{1}{a}>\frac{1}{b}$ | B. | 若$\frac{1}{a}>1$,则0<a<1 | C. | 若a>b>0,则a4>b4 | D. | 若a<1,则$\frac{1}{a}<1$ |
17.从1,2,3,4,5这5个数字中任选2个数字,则这2个数字之和为偶数的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
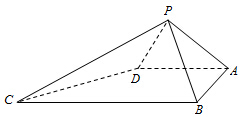 四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BCD=45°.△PAB与△PAD都是等边三角形.
四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BCD=45°.△PAB与△PAD都是等边三角形.