Question

6．已知数列{a_n}是公差不为0的等差数列，a₁=$\frac{1}{2}$，数列{b_n}是等比数列，且b₁=a₁，b₂=a₃，b₃=a₄，数列{b_n}的前n项和为S_n．记点Q_n（b_n，S_n），n∈Z⁺．
（1）求数列{a_n}，{b_n}的通项公式；
（2）证明点Q₁，Q₂，Q₃，…，Q_n…在同一条直线l上，并求出直线l的方程；
（3）若△OQ_nQ_n+1，（n∈Z⁺）的面积为A_n，T_n为数列{A_n}的前n项和之和，求：$\underset{lim}{n→∞}$A_n及$\underset{lim}{n→∞}$T_n．

Answer 1

分析 （1）设a_n=$\frac{1}{2}$+（n-1）d，从而可得（$\frac{1}{2}$+2d）²=$\frac{1}{2}$（$\frac{1}{2}$+3d），从而解得；
（2）由（1）知S_n=$\frac{\frac{1}{2}（1-（\frac{1}{2}）^{n}）}{1-\frac{1}{2}}$=1-（$\frac{1}{2}$）ⁿ，从而可得点Q_n（（$\frac{1}{2}$）ⁿ，1-（$\frac{1}{2}$）ⁿ），从而证明并得到直线方程．
（3）由题意作图，从而结合图象写出即可．

解答 解：（1）由题意设a_n=$\frac{1}{2}$+（n-1）d，
则b₁=a₁=$\frac{1}{2}$，b₂=a₃=$\frac{1}{2}$+2d，b₃=a₄=$\frac{1}{2}$+3d，
∵数列{b_n}是等比数列，
∴（$\frac{1}{2}$+2d）²=$\frac{1}{2}$（$\frac{1}{2}$+3d），
∴d=-$\frac{1}{8}$，q=$\frac{\frac{1}{4}}{\frac{1}{2}}$=$\frac{1}{2}$，
故a_n=$\frac{1}{2}$-（n-1）$\frac{1}{8}$=$\frac{5-n}{8}$，
则b_n=$\frac{1}{2}$•（$\frac{1}{2}$）^n-1=（$\frac{1}{2}$）ⁿ；
（2）证明：由（1）知，
S_n=$\frac{\frac{1}{2}（1-（\frac{1}{2}）^{n}）}{1-\frac{1}{2}}$=1-（$\frac{1}{2}$）ⁿ，
故点Q_n（（$\frac{1}{2}$）ⁿ，1-（$\frac{1}{2}$）ⁿ），
∵（$\frac{1}{2}$）ⁿ+1-（$\frac{1}{2}$）ⁿ=1，
∴点Q₁，Q₂，Q₃，…，Q_n…都在直线x+y=1上，
即l的方程为x+y-1=0；
（3）由题意作图如下，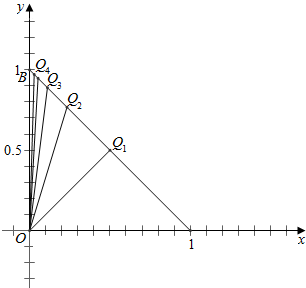
，
结合图象可知，
$\underset{lim}{n→∞}$A_n=0，$\underset{lim}{n→∞}$T_n=${S}_{△O{Q}_{1}B}$=$\frac{1}{2}×\frac{1}{2}×1×1$=$\frac{1}{4}$．

点评 本题考查了等差数列与等比数列的应用，同时考查了数形结合的思想应用．