题目内容
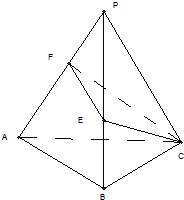 如图.P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,若PA=
如图.P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,若PA=| 5 |
| 10 |
| 2 |
(Ⅰ)求证:△ABC为锐角三角形;
(Ⅱ)求多面体ECAB的体积.
考点:棱柱、棱锥、棱台的体积
专题:综合题
分析:(Ⅰ)由题意作PD垂直AB于D,连结CD,由线面垂直的定义和判定定理证明AB⊥CD,得∠CAB与∠CBA都是锐角,同理∠ACB是锐角,即可证明△ABC为锐角三角形;
(Ⅱ)根据几何体的特点利用割补法将多面体ECAB的体积表示出来,再由三棱锥的体积公式和条件求出多面体ECAB的体积.
(Ⅱ)根据几何体的特点利用割补法将多面体ECAB的体积表示出来,再由三棱锥的体积公式和条件求出多面体ECAB的体积.
解答:
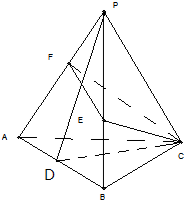 (Ⅰ)证明:过点P作PD垂直AB于D,连结CD,
(Ⅰ)证明:过点P作PD垂直AB于D,连结CD,
∵PC⊥PA,PC⊥PB,PB∩PA=P,
∴PC⊥平面PAB,
∵AB?平面ABC,∴AB⊥PC,
又∵PD⊥AB,且PC∩PD=P
∴AB⊥平面PDC,
∵CD?平面ABC,∴AB⊥CD,
∴∠CAB与∠CBA都是锐角,
同理∠ACB是锐角,
∴△ABC为锐角三角形,
(Ⅱ)由(Ⅰ)得,PC⊥平面PAB,
∵PA⊥PB,且PA=
PB=
PC=2
,
∴△PAB的面积S△PAB=
×PA×PB=
,PC=
,
∵PE:EB=1:2,PF:FA=2:3
∴△PEF的面积S△PEF=
×PE×PF=
×
×PA×
×PB=
×
,
则VC-BEFA=VC-PAB-VC-PEF=
×S△PAB×PC-
×S△PEF×PC
=
×
×
×
=
.
 (Ⅰ)证明:过点P作PD垂直AB于D,连结CD,
(Ⅰ)证明:过点P作PD垂直AB于D,连结CD,∵PC⊥PA,PC⊥PB,PB∩PA=P,
∴PC⊥平面PAB,
∵AB?平面ABC,∴AB⊥PC,
又∵PD⊥AB,且PC∩PD=P
∴AB⊥平面PDC,
∵CD?平面ABC,∴AB⊥CD,
∴∠CAB与∠CBA都是锐角,
同理∠ACB是锐角,
∴△ABC为锐角三角形,
(Ⅱ)由(Ⅰ)得,PC⊥平面PAB,
∵PA⊥PB,且PA=
| 5 |
| 10 |
| 2 |
∴△PAB的面积S△PAB=
| 1 |
| 2 |
4
| ||
| 5 |
2
| ||
| 5 |
∵PE:EB=1:2,PF:FA=2:3
∴△PEF的面积S△PEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 5 |
| 2 |
| 15 |
4
| ||
| 5 |
则VC-BEFA=VC-PAB-VC-PEF=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 13 |
| 15 |
4
| ||
| 5 |
2
| ||
| 5 |
| 104 |
| 225 |
点评:本题考查了线面垂直的定义和判定定理的应用,三棱锥的体积公式,以及割补法求不规则几何体的体积.

练习册系列答案
相关题目