题目内容
2．当0＜a＜1时，函数y=loga（x2-4x+3）的单调增区间为（ ）| A． | （-∞，2] | B． | [2，+∞） | C． | （-∞，1） | D． | （3，+∞） |
分析 令t=x2-4x+3＞0，求得函数的定义域，根据0＜a＜1，y=logat，本题即求函数t的减区间，再利用二次函数的性值可得结论．
解答 解：令t=x2-4x+3＞0，求得x＜1，或 x＞3，可得函数的定义域为{x|x＜1，或 x＞3}，
又0＜a＜1，y=logat，故本题即求函数t的减区间．
再利用二次函数的性值可得函数t的减区间为（-∞，1），
故选：C．
点评 本题主要考查复合函数的单调性，对数函数、二次函数的性质，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
4．设集合A={x|x2-3x＜0}，B={x|x2＞4}，则A∩B=（ ）
| A． | （-2，0） | B． | （-2，3） | C． | （0，2） | D． | （2，3） |
10．
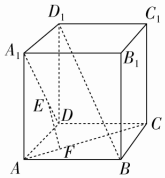如图所示，在正方体ABCD-A1B1C1D1中，E、F分别在A1D、AC上，且A1E=$\frac{2}{3}$A1D，AF=$\frac{1}{3}$AC，则（ ）
如图所示，在正方体ABCD-A1B1C1D1中，E、F分别在A1D、AC上，且A1E=$\frac{2}{3}$A1D，AF=$\frac{1}{3}$AC，则（ ）| A． | EF至多与A1D、AC之一垂直 | B． | EF与A1D、AC都垂直 | ||
| C． | EF与BD1相交 | D． | EF与BD1异面 |
7．函数f（x）=3-sinx-2cos2x，$x∈[{\frac{π}{6}，\frac{7π}{6}}]$，则函数的最大值与最小值之差为（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{5}{8}$ | C． | $\frac{7}{8}$ | D． | $\frac{9}{8}$ |