题目内容
15.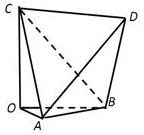 如图,多面体OABCD,AB=CD=2,AD=BC=$2\sqrt{3}$,AC=BD=$\sqrt{10}$,且OA,OB,OC两两垂直,则下列说法正确的是( )
如图,多面体OABCD,AB=CD=2,AD=BC=$2\sqrt{3}$,AC=BD=$\sqrt{10}$,且OA,OB,OC两两垂直,则下列说法正确的是( )| A. | 直线OB∥平面ACD | |
| B. | 球面经过点A、B、C、D四点的球的直径是$\sqrt{13}$ | |
| C. | 直线AD与OB所成角是45° | |
| D. | 二面角A-OC-D等于30° |
分析 对四个选项分别进行判断,即可得出结论.
解答 解:对于A,由于OB∥AE,AE和平面ACD相交,则OB和平面ACD相交,故A错
对于B,球面经过点A、B、C、D两点的球的直径即为长方体的对角线长,
即为$\sqrt{1+9+3}$=$\sqrt{13}$,故B对
对于C由于OB∥AE,则∠DAE即为直线AD与OB所成的角,tan∠DAE=$\sqrt{3}$,则∠DAE=60°,故C错误;
对于D,因为AO⊥OC,DC⊥OC,所以异面直线CD与OA所成的角大小为二面角A-OC-D的二面角大小,连接OE,则∠AOE为所求,tan∠AOE=$\sqrt{3}$,所以∠AOE=60°;D错误.
故选B.
点评 本题考查线面的位置关系的判断,空间异面直线所成的角,以及多面体的外接球的关系,考查运算能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
5.A=$\left\{{(x,y)\left|{y≤\left.{\sqrt{4-{x^2}},y≥0}\right\}}\right.}$,B={(x,y)|x+y≥2},则A∩B所对应区域面积为( )
| A. | 2π | B. | π-2 | C. | π | D. | π+2 |
5.在空间,α表示平面,m,n表示二条直线,则下列命题中错误的是( )
| A. | 若m∥α,m、n不平行,则n与α不平行 | B. | 若m∥α,m、n不垂直,则n与α不垂直 | ||
| C. | 若m⊥α,m、n不平行,则n与α不垂直 | D. | 若m⊥α,m、n不垂直,则n与α不平行 |