A=$\left\{{(x.y)\left|{y≤\left.{\sqrt{4-{x^2}}.y≥0}\right\}}\right.}$.B={(x.y)|x+y≥2}.则A∩B所对应区域面积为( )A．2πB．π-2C．πD．π+2 题目和参考答案——青夏教育精英家教网—

题目内容

5．A=$\left\{{（x，y）\left|{y≤\left.{\sqrt{4-{x^2}}，y≥0}\right\}}\right.}$，B={（x，y）|x+y≥2}，则A∩B所对应区域面积为（　　）

A．

2π

B．

π-2

C．

D．

π+2

分析由题意作出图象，然根据面积公式计算即可得答案．

解答解：由A=$\left\{{（x，y）\left|{y≤\left.{\sqrt{4-{x^2}}，y≥0}\right\}}\right.}$，B={（x，y）|x+y≥2}，则A∩B所对应区域面积为如图阴影部分的面积，
则为$\frac{1}{4}$π×4-$\frac{1}{2}×2×2$=π-2，
故选：B

点评本题考查了二元一次不等式表示的平面区域，体现了数学转化思想方法，是中档题

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

16．数列{a_n}中，若a_n+1=$\frac{{a}_{n}}{2{a}_{n}+1}$，a₁=1，则a₆等于$\frac{1}{11}$．

13．过点$P（{\sqrt{2}，0}）$与圆x²+y²=1相切的直线方程为$x-y-\sqrt{2}=0或x+y-\sqrt{2}=0$．

20．等差数列{a_n}的前10项和为30，前20项和为100，则它的前30项和是（　　）

10．（1）求函数f（x）=3tan（$\frac{π}{6}$-$\frac{x}{4}$）的周期和单调递减区间；
（2）试比较f（π）与f（$\frac{3π}{2}$）的大小．

17．已知直线l?平面α，直线m?平面α，下面四个结论：①若l⊥α，则l⊥m；②若l∥α，则l∥m；③若l⊥m，则l⊥α；④若l∥m，则l∥α，其中正确的是（　　）

14．不等式x|x-1|＞0的解集为（0，1）∪（1，+∞）．

15．

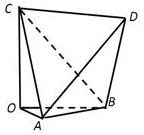如图，多面体OABCD，AB=CD=2，AD=BC=$2\sqrt{3}$，AC=BD=$\sqrt{10}$，且OA，OB，OC两两垂直，则下列说法正确的是（　　）

	A．	直线OB∥平面ACD
	B．	球面经过点A、B、C、D四点的球的直径是$\sqrt{13}$
	C．	直线AD与OB所成角是45°
	D．	二面角A-OC-D等于30°

试题分类