题目内容
6．已知函数f（x）=$\frac{6}{x-1}$-$\sqrt{x+4}$，求函数f（x）的定义域[-4，1）∪（1，+∞）．分析 根据二次根式的性质以及分母不是0，求出函数的定义域即可．
解答 解：由题意得：$\left\{\begin{array}{l}{x-1≠0}\\{x+4≥0}\end{array}\right.$，
解得：x≥-4或x≠1，
故答案为：[-4，1）∪（1，+∞）．
点评 本题考查了求函数的定义域问题，考查二次根式的性质，是一道基础题．
练习册系列答案
相关题目
1．若$\left\{{1，a，\frac{b}{a}}\right\}=\left\{{0，{a^2}，a+b}\right\}$，则a2017+b2017的值为（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 1或-1 |
18．幂函数y=x-1不具有的特性是 （ ）
| A． | 在定义域内是减函数 | B． | 图象过定点（1，1） | ||
| C． | 是奇函数 | D． | 其定义域是R |
15．
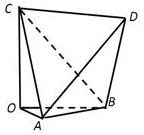如图，多面体OABCD，AB=CD=2，AD=BC=$2\sqrt{3}$，AC=BD=$\sqrt{10}$，且OA，OB，OC两两垂直，则下列说法正确的是（ ）
如图，多面体OABCD，AB=CD=2，AD=BC=$2\sqrt{3}$，AC=BD=$\sqrt{10}$，且OA，OB，OC两两垂直，则下列说法正确的是（ ）| A． | 直线OB∥平面ACD | |
| B． | 球面经过点A、B、C、D四点的球的直径是$\sqrt{13}$ | |
| C． | 直线AD与OB所成角是45° | |
| D． | 二面角A-OC-D等于30° |