题目内容
15.已知矩形ABEF所在的平面与矩形ABCD所在的平面互相垂直,AD=2,AB=3,AF=$\frac{{3\sqrt{3}}}{2}$,M为EF的中点,则多面体M-ABCD的外接球的表面积为16π.分析 设球心到平面ABCD的距离为d,利用矩形ABEF所在的平面与矩形ABCD所在的平面互相垂直,AF=$\frac{{3\sqrt{3}}}{2}$,M为EF的中点,可得M到平面ABCD的距离为$\frac{{3\sqrt{3}}}{2}$,从而R2=($\frac{\sqrt{4+9}}{2}$)2+d2=12+($\frac{{3\sqrt{3}}}{2}$-d)2,求出R2=4,即可求出多面体E-ABCD的外接球的表面积.
解答 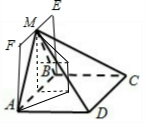 解:设球心到平面ABCD的距离为d,
解:设球心到平面ABCD的距离为d,
∵矩形ABEF所在的平面与矩形ABCD所在的平面互相垂直,AF=$\frac{{3\sqrt{3}}}{2}$,M为EF的中点,
∴M到平面ABCD的距离为$\frac{{3\sqrt{3}}}{2}$,
∴R2=($\frac{\sqrt{4+9}}{2}$)2+d2=12+($\frac{{3\sqrt{3}}}{2}$-d)2,
∴d=$\frac{\sqrt{3}}{2}$,R2=4,
∴多面体E-ABCD的外接球的表面积为4πR2=16π.
故答案为:16π.
点评 本题考查多面体E-ABCD的外接球的表面积,考查学生的计算能力,正确求出多面体E-ABCD的外接球的半径是关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
6.小赵、小钱、小孙、小李到 4 个景点旅游,每人只去一个景点,设事件 A=“4 个人去的景点不相同”,事件B=“小赵独自去一个景点”,则P( A|B)=( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
10.已知$P:{x^2}-2x<0,Q:\frac{x+3}{x-1}≤0$,若P真Q假,则x的取值范围是( )
| A. | [1,2) | B. | (1,2) | C. | (-∞,-3) | D. | (-∞,-3] |
5.已知集合 A={x|x2-x-2>0},B={x|1≤x≤3},则 A∩B=( )
| A. | [1,3] | B. | (1,3] | C. | [2,3] | D. | (2,3] |