题目内容
3.某校今年计划招聘女教师x人,男教师y人,若x、y满足$\left\{\begin{array}{l}{2x-y≥5}\\{x-y≤2}\\{x<6}\end{array}\right.$,则该学校今年计划招聘教师最多10人.分析 作出不等式组对应的平面区域,则目标函数为z=x+y,利用线性规划的知识进行求解即可.
解答 解:设z=x+y,
作出不等式组对应的平面区域如图:
由z=x+y得y=-x+z,
平移直线y=-x+z,
由图象可知当直线y=-x+z经过点A时,
直线y=-x+z的截距最大,
此时z最大.但此时z最大值取不到,
由图象当直线经过整点E(5,5)时,z=x+y取得最大值,
代入目标函数z=x+y得z=5+5=10.
即目标函数z=x+y的最大值为10.
故答案为:10.
点评 本题主要考查线性规划的应用问题,根据图象确定最优解,要根据整点问题进行调整,有一定的难度.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
14.若$f(x)=cos2x+acos({\frac{π}{2}+x})$在区间$({\frac{π}{6},\frac{π}{2}})$上是增函数,则实数a的取值范围为( )
| A. | [-2,+∞) | B. | (-2,+∞) | C. | (-∞,-4) | D. | (-∞,-4] |
18.从数字1,2,3,4中任取两个不同的数字构成一个两位数,这个两位数大于20的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
12.已知α是第一象限角,满足$sinα-cosα=\frac{{\sqrt{10}}}{5}$,则cos2α=( )
| A. | -$\frac{3}{5}$ | B. | $±\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $±\frac{4}{5}$ |
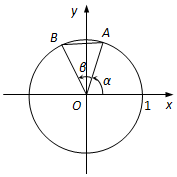 如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB=$\frac{{2\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB=$\frac{{2\sqrt{5}}}{5}$.