题目内容
5.已知数列{an}为等差数列,其中a2+a3=8,a5=3a2.(1)求数列{an}的通项公式;
(2)记${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}$,设{bn}的前n项和为Sn.求最小的正整数n,使得${S_n}>\frac{2016}{2017}$.
分析 (1)设等差数列{an}的公差为d,运用等差数列的通项公式可得首项和公差的方程,解方程可得首项和公差,进而得到通项公式;
(2)求得${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}$=$\frac{2}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}$-$\frac{1}{2n+1}$,运用数列的求和方法:裂项相消求和,再解不等式,即可得到所求n的最小值.
解答 解:(1)设等差数列{an}的公差为d,
依a2+a3=8,a5=3a2,
有$\left\{\begin{array}{l}2{a_1}+3d=8\\{a_1}+4d=3{a_1}+3d\end{array}\right.$,
解得a1=1,d=2,
从而{an}的通项公式为${a_n}=2n-1,n∈{N^*}$;
(2)因为${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}$=$\frac{2}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}$-$\frac{1}{2n+1}$,
所以 ${S_n}=({\frac{1}{1}-\frac{1}{3}})+({\frac{1}{3}-\frac{1}{5}})+…+({\frac{1}{2n-1}-\frac{1}{2n+1}})$
=$1-\frac{1}{2n+1}$.
令 $1-\frac{1}{2n+1}>\frac{2016}{2017}$,
解得n>1008,
故n的最小值为1009.
点评 本题考查等差数列的通项公式的运用,注意运用方程思想,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.


| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{16π}{3}$ |
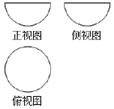 如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )
如图是某几何体的三视图,其正视图,侧视图均为直径为2的半圆,俯视图是直径为2的圆,则该几何体的表面积为( )| A. | 3π | B. | 4π | C. | 5π | D. | 12π |
| A. | $81-27\sqrt{3}$ | B. | 54 | C. | 38-1 | D. | 80 |
| A. | [-2,+∞) | B. | (-2,+∞) | C. | (-∞,-4) | D. | (-∞,-4] |
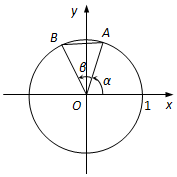 如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB=$\frac{{2\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB=$\frac{{2\sqrt{5}}}{5}$.