题目内容
20.已知两个单位向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{7}$.分析 根据平面向量数量积的定义与模长公式,求出结果即可.
解答 解:两个单位向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=1×1×cos60°=$\frac{1}{2}$,
∴${(\overrightarrow{a}+2\overrightarrow{b})}^{2}$=${\overrightarrow{a}}^{2}$+4$\overrightarrow{a}$•$\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$
=1+4×$\frac{1}{2}$+4×1
=7,
∴|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查了平面向量数量积的定义与模长公式的应用问题,是基础题目.

练习册系列答案
相关题目
10.已知等比数列{an}的公比为正数,前n项和为Sn,a1+a2=2,a3+a4=6,则S8等于( )
| A. | $81-27\sqrt{3}$ | B. | 54 | C. | 38-1 | D. | 80 |
5.已知函数$f(x)=\left\{\begin{array}{l}\sqrt{x}+3,x≥0\\ ax+b,x<0\end{array}\right.$满足条件:对于?x1∈R,且x1≠0,?唯一的x2∈R且x1≠x2,使得f(x1)=f(x2).当f(2a)=f(3b)成立时,则实数a+b=( )
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $-\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{6}}}{2}$+3 | D. | $-\frac{{\sqrt{6}}}{2}$+3 |
12.已知α是第一象限角,满足$sinα-cosα=\frac{{\sqrt{10}}}{5}$,则cos2α=( )
| A. | -$\frac{3}{5}$ | B. | $±\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $±\frac{4}{5}$ |
9.据统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学学习时间x与数学成绩y进行数据收集如表:
由表中样本数据求回归直线方程$\stackrel{∧}{y}$=bx+a,则点(a,b)与直线x+18y=110的位置关系为是( )
| x | 15 | 16 | 18 | 19 | 22 |
| y | 102 | 98 | 115 | 115 | 120 |
| A. | 点在直线左侧 | B. | .点在直线右侧 | C. | .点在直线上 | D. | 无法确定 |
10.下方茎叶图如图1,为高三某班50名学生的数学考试成绩,算法框图如图2中输入的ai为茎叶图中的学生成绩,则输出的m,n分别是( )
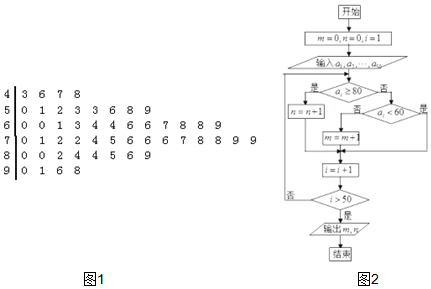

| A. | m=26,n=12 | B. | m=38,n=12 | C. | m=12,n=12 | D. | m=24,n=10 |