题目内容
3．
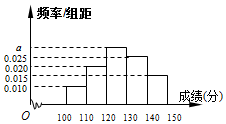某学校对高二年级期中考试数学成绩进行分析，随机抽取了分数在[100，150]的1000名学生的成绩，并根据这1000名学生的成绩画出频率分布直方图（如图所示），则成绩在[120，130）内的学生共有300人．
分析 根据频率和为1，求出成绩在[120，130）内的频率与频数即可．
解答 解：根据频率和为1，得成绩在[120，130）内的频率为
1-（0.010+0.020+0.025+0.015）×10=0.3，
所以成绩在[120，130）内的学生共有
1000×0.3=300．
故答案为：300．
点评 本题考查了频率分布直方图的应用问题，是基础题目．
练习册系列答案
相关题目
14．如果函数y=sin（x+ϕ）的图象经过点$（\frac{π}{3}，0）$，那么ϕ可以是（ ）
| A． | 0 | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
15．设函数f（x）=ax2+bx+c（a＞b＞c）的图象经过点A（m1，f（m1））和点B（m2，f（m2）），f（1）=0，若a2+（f（m1）+f（m2）•a+f（m1）•f（m2）=0，则（ ）
| A． | b≥0 | B． | b＜0 | C． | 3a+c≤0 | D． | 3a-c＜0 |
14．已知$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$，且$\overrightarrow{OA}•\overrightarrow{OB}=0$，点C在∠AOB内，$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为30°，若$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$，（m，n∈R），则$\frac{n}{m}$的值为（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\frac{{\sqrt{2}}}{2}$ |