题目内容
某幸运观众参加电视节目抽奖活动,抽奖规则是:在盒子里预先放有大小相同的5个小球,其中一个绿球,两个红球,两个白球.该观众依次从盒子里摸球,每次摸一个球(不放回),若累计摸到两个白球就停止摸球,否则直到将盒子里的球摸完才停止.规定:在球摸停止时,只有摸出红球才获得奖金,奖金数为摸出红球个数的1000倍(单位:元).
(Ⅰ)求该幸运观众摸三次球就停止的概率;
(Ⅱ)求该幸运观众获得1000元奖金的概率.
解(Ⅰ)由题意知本题是一个古典概型,
试验发生包含的事件是摸球三次共有A53种结果,
满足条件的事件是该幸运观众摸三次球就停止,共有C21C31A22
记“该幸运观众摸球三次就停止”为事件A,
∴根据古典概型的概率公式得到P(A)=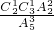 =
= .
.
(Ⅱ)由题意知本题是一个古典概型和互斥事件的概率,
该幸运观众获得1000元奖金包括两种情况,一是摸三次停止,二是模4次停止
这两种情况是互斥的,每一种情况是一个古典概型,
三次停止的概率第一问已经做出,四次停止的概率是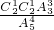
∴该幸运观众获得1000元奖金的概率为P=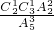 +
+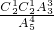 =
= .
.
分析:(Ⅰ)本题是一个古典概型,试验发生包含的事件是摸球三次共有A53种结果,满足条件的事件是该幸运观众摸三次球就停止,共有C21C31A22,根据古典概型概率公式得到结果.
(Ⅱ)本题是古典概型和互斥事件的概率,该幸运观众获得1000元奖金包括两种情况,一是摸三次停止,二是模4次停止这两种情况是互斥的,每一种情况是一个古典概型,根据上一问做出的结果方法,得到结果.
点评:本题考查古典概型的概率公式,考查互斥事件的概率,本题是一个基础题,题目的运算量不大,题意也比较好理解,是一个送分题目.
试验发生包含的事件是摸球三次共有A53种结果,
满足条件的事件是该幸运观众摸三次球就停止,共有C21C31A22
记“该幸运观众摸球三次就停止”为事件A,
∴根据古典概型的概率公式得到P(A)=
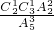 =
= .
.(Ⅱ)由题意知本题是一个古典概型和互斥事件的概率,
该幸运观众获得1000元奖金包括两种情况,一是摸三次停止,二是模4次停止
这两种情况是互斥的,每一种情况是一个古典概型,
三次停止的概率第一问已经做出,四次停止的概率是
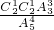
∴该幸运观众获得1000元奖金的概率为P=
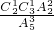 +
+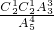 =
= .
.分析:(Ⅰ)本题是一个古典概型,试验发生包含的事件是摸球三次共有A53种结果,满足条件的事件是该幸运观众摸三次球就停止,共有C21C31A22,根据古典概型概率公式得到结果.
(Ⅱ)本题是古典概型和互斥事件的概率,该幸运观众获得1000元奖金包括两种情况,一是摸三次停止,二是模4次停止这两种情况是互斥的,每一种情况是一个古典概型,根据上一问做出的结果方法,得到结果.
点评:本题考查古典概型的概率公式,考查互斥事件的概率,本题是一个基础题,题目的运算量不大,题意也比较好理解,是一个送分题目.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
通过随机询问100名性别不同的大学生是否爱好踢毪子运动,得到如下的列联表:
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
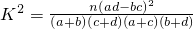 ,经计算,统计量K2的观测值k≈4.762,参照附表,得到的正确结论是
,经计算,统计量K2的观测值k≈4.762,参照附表,得到的正确结论是- A.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
- B.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
- C.有97.5%以上的把握认为“爱好该项运动与性别有关”
- D.有97.5%以上的把握认为“爱好该项运动与性别无关”
 =(sinA,cos2A),
=(sinA,cos2A), =(2cosA,1),f(A)=
=(2cosA,1),f(A)= 如图所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC=________.
如图所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC=________.

 ,
, ,
, 、
、 的夹角为
的夹角为 ,
, ,则△AOB的最大面积是________.
,则△AOB的最大面积是________. 的左、右焦点,P为椭圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点距离为________.
的左、右焦点,P为椭圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点距离为________. |的最小正周期是π;
|的最小正周期是π; x的图象的对称中心是(kπ,0),k∈Z;
x的图象的对称中心是(kπ,0),k∈Z; ),k∈Z;
),k∈Z;