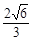题目内容

设F₁、F₂分别是椭圆 $数学公式$ 的左、右焦点，P为椭圆上一点，M是F₁P的中点，|OM|=3，则P点到椭圆左焦点距离为________．

4
分析：由题意知，OM是三角形PF₁P的中位线，由|OM|=3，可得|PF₂|=6，再由椭圆的定义求出|PF₁|的值．
解答：由题意知，OM是三角形PF₁P的中位线，
∵|OM|=3，∴|PF₂|=6，
又|PF₁|+|PF₂|=2a=10，
∴|PF₁|=4，
故答案为4．
点评：本题考查椭圆的定义，以及椭圆的简单性质的应用，判断OM是三角形PF₁P的中位线是解题的关键．

练习册系列答案

三点一测系列答案

小天才课时作业系列答案

一课四练系列答案

黄冈小状元满分冲刺微测验系列答案

新辅教导学系列答案

初中自主学习课时集训系列答案

阳光同学一线名师全优好卷系列答案

过关冲刺100分系列答案

圆梦图书课时达标100分系列答案

高效作业系列答案

相关题目

=1(a＞b＞0)短轴长为2，P（x₀，y₀）（x₀≠±a）是椭圆上一点，A，B分别是椭圆的左、右顶点，直线PA，PB的斜率之积为-

．
（1）求椭圆的方程；
（2）当∠F₁PF₂为钝角时，求P点横坐标的取值范围；
（3）设F₁，F₂分别是椭圆的左右焦点，M、N是椭圆右准线l上的两个点，若

=0，求MN的最小值．

（09年丰台区二模）（14分）

设F₁、F₂分别是椭圆的左、右焦点。

（I）若M是该椭圆上的一个动点，求的最大值和最小值；

（II）设过定点（0，2）的直线l与椭圆交于不同两点A、B，且∠AOB为钝角（其中O为坐标原点），求直线l的斜率k的取值范围。

设F₁、F₂分别是椭圆的左、右焦点，P为椭圆上一点，M是F₁P的中点，|OM|＝3，则P点到椭圆左焦点距离为 .

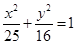设F₁、F₂分别是椭圆的左、右焦点，P为椭圆上任一点，点M的坐标为(6,4)，则|PM|＋|PF₁|的最大值为_______

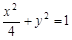设F₁，F₂分别是椭圆的左、右焦点，P是第一象限内该椭圆上的一点，且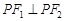，求点P的横坐标为（）

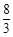A．1 B． C． D．