题目内容
设函数f(x)=lg(x2+ax﹣a﹣1),给出下述命题:
①函数f(x)的值域为R;②函数f(x)有最小值;
③当a=0时,函数f(x)为偶函数;④若f(x)在区间[2,+∞)上单调递增,则实数a的取值范围a≥﹣4.
正确的命题是( )
|
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
A
解:∵u=x2+ax﹣a﹣1的最小值为﹣ (a2+4a+4)≤0∴①函数f(x)的值域为R为真命题;
(a2+4a+4)≤0∴①函数f(x)的值域为R为真命题;
但函数f(x)无最小值,故②错误;当a=0时,易得f(﹣x)=f(x),即③函数f(x)为偶函数正确;
若f(x)在区间[2,+∞)上单调递增,则 解得a>﹣3,故④错误;故选A
解得a>﹣3,故④错误;故选A

练习册系列答案
相关题目
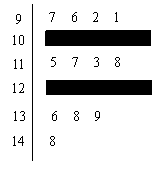
某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
| 分数段(分) | |
|
|
| 频数 | 4 | ||
| 频率 | | 0.45 | 0.2 |
(Ⅰ)求表中 的值及分数在
的值及分数在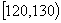 范围内的学生人数;
范围内的学生人数;
(Ⅱ)从得分在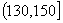 内的学生随机选2名学生的得分,求2名学生的平均分不低
内的学生随机选2名学生的得分,求2名学生的平均分不低
于140分的概率.

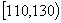
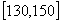
 ,
, (
( ),若对
),若对 ,
, ,使得
,使得 ,则实数
,则实数 ,
, 的取值范围是( )
的取值范围是( ) ,
, B.
B. C.
C. ,
, ,
, ,Q=
,Q= ;若将
;若将 ,lgQ,lgP适当排序后可构成公差为1的等差数列
,lgQ,lgP适当排序后可构成公差为1的等差数列 的前三项.(1)试比较M、P、Q的大小; (2)求
的前三项.(1)试比较M、P、Q的大小; (2)求 的值及
的值及 的图象在
的图象在 轴上截得的线段长为
轴上截得的线段长为 ,设
,设
 ,求
,求 ,并证明
,并证明 .
. 的反函数
的反函数 ________________.
________________.  的部分图象大致是 ( )
的部分图象大致是 ( )
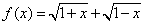 。 (1)求函数
。 (1)求函数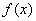 的定义域和值域;
的定义域和值域;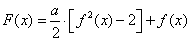 (
(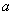 为实数),求
为实数),求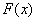 在
在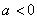 时的最大值
时的最大值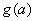 ;
;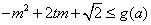 对
对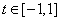 恒成立,求实数
恒成立,求实数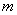 的取值范围。
的取值范围。 现有四个
现有四个 命题:
命题: ,则
,则 ;
;


 题有________________
题有________________
 __.(写出所
__.(写出所 有真命题的编号)
有真命题的编号)