题目内容
已知函数 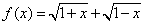 。 (1)求函数
。 (1)求函数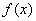 的定义域和值域;
的定义域和值域;
(2)设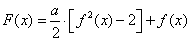 (
(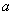 为实数),求
为实数),求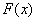 在
在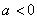 时的最大值
时的最大值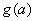 ;
;
(3)对(2)中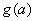 ,若
,若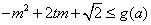 对
对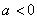 所有的实数
所有的实数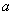 及
及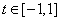 恒成立,求实数
恒成立,求实数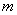 的取值范围。
的取值范围。
解: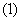 由1+x≥0且1-x≥0,得-1≤x≤1,所以定义域为
由1+x≥0且1-x≥0,得-1≤x≤1,所以定义域为 …………2分
…………2分
又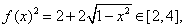 由
由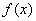 ≥0 得值域为
≥0 得值域为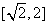 …………4分
…………4分
( 2)因为
2)因为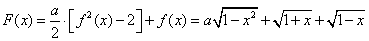
令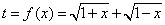 ,则
,则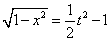 ,
,
∴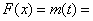
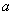 (
(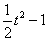 )+t=
)+t=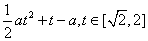 …………6分
…………6分
由题意知g(a)即为函数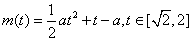 的最大值。
的最大值。
注意到直线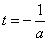 是抛物线
是抛物线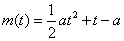 的对称轴。…………7分
的对称轴。…………7分
因为a<0时,函数y=m(t), 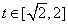 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
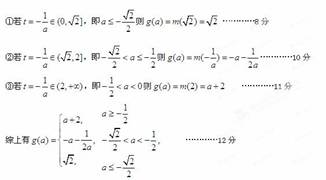 (3)易得
(3)易得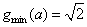 , ………14分
, ………14分
由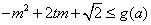 对
对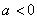 恒成立,即要使
恒成立,即要使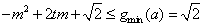 恒成立,…………15分
恒成立,…………15分
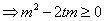 ,令
,令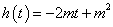 ,对所有的
,对所有的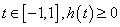 成立,
成立,
只需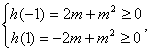 …17分求出m的取值范围是
…17分求出m的取值范围是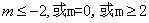 . …………18分
. …………18分

练习册系列答案
相关题目
 在定义域的某个子区间
在定义域的某个子区间 上不存在反函数,则
上不存在反函数,则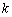 的取值范围是 _____.
的取值范围是 _____.  ,若区间
,若区间 上
上 的最大值称为
的最大值称为 在
在 上的“绝对差”为
上的“绝对差”为 B.
B. C.
C. D.
D.
 上的函数
上的函数 满足
满足 ,若关于x的方程
,若关于x的方程 有5个不同实根,则正实数
有5个不同实根,则正实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 成立,则实数
成立,则实数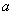 的取值范围是 ( )
的取值范围是 ( ) B.
B.  C.
C.  D.
D. 
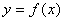 的图象与直线
的图象与直线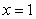 的交点个数为0或1;
的交点个数为0或1;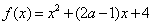 , 若当
, 若当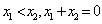 时,总有
时,总有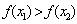 ,则
,则 ;
;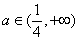 时,函数
时,函数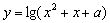 的值域为
的值域为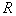 ;
;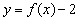 的图象关于点
的图象关于点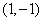 对称的图象对应的函数为
对称的图象对应的函数为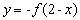 .
. , 则该函数在
, 则该函数在 上是 ( )
上是 ( )  单调递减无最小值
单调递减无最小值  单调递减有最小值
单调递减有最小值  单调递增无最大值
单调递增无最大值  单调递增有最大值
单调递增有最大值