题目内容
16.已知O是坐标原点,点A(1,0),若点M(x,y)为平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$上的一个动点,则|$\overrightarrow{OA}$+$\overrightarrow{OM}$|的取值范围是( )| A. | [$\sqrt{5}$,2$\sqrt{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{3\sqrt{2}}{2}$,2$\sqrt{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
分析 由题意作出可行域,由向量的坐标加法运算求得$\overrightarrow{OA}$+$\overrightarrow{OM}$的坐标,把|$\overrightarrow{OA}$+$\overrightarrow{OM}$|转化为可行域内的点M(x,y)到定点D(-1,0)的距离,数形结合可得答案.
解答 解:∵点A(1,0),点M(x,y),
∴$\overrightarrow{OA}$+$\overrightarrow{OM}$=(1+x,y),
设z=|$\overrightarrow{OA}$+$\overrightarrow{OM}$|=$\sqrt{(1+x)^{2}+{y}^{2}}$,
则z的几何意义为M到定点D(-1,0)的距离,
由约束条件作平面区域如图,
由图象可知当M位于A(1,2)时,z取得最大值z=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
当M位于E时,z取得最小值z=$\frac{|-1+0-2|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$
即|$\overrightarrow{OA}$+$\overrightarrow{OM}$|的取值范围是[$\frac{3\sqrt{2}}{2}$,2$\sqrt{2}$],
故选:C
点评 本题考查了简单的线性规划,考查了数形结合、转化与化归等解题思想方法,考查了向量模的求法,是中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
4.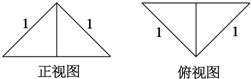 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
11.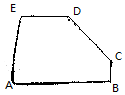 如图所示的五边形是由一个矩形截去一个角而得,且BC=1,DE=2,AE=3,AB=4,则$\overrightarrow{CD}$等于( )
如图所示的五边形是由一个矩形截去一个角而得,且BC=1,DE=2,AE=3,AB=4,则$\overrightarrow{CD}$等于( )
 如图所示的五边形是由一个矩形截去一个角而得,且BC=1,DE=2,AE=3,AB=4,则$\overrightarrow{CD}$等于( )
如图所示的五边形是由一个矩形截去一个角而得,且BC=1,DE=2,AE=3,AB=4,则$\overrightarrow{CD}$等于( )| A. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AE}$ | B. | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AE}$ | C. | -$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AE}$ | D. | -$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AE}$ |
1.由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理叫( )
| A. | 合情推理 | B. | 演绎推理 | C. | 类比推理 | D. | 归纳推理 |
8.在一个游戏中,有两枚大小相同、质地均匀的正四面体骰子,每个面上分别写着数字1,2,3,5.同时投掷一次,记x为两个朝下的面上的数字之和,则x不小于6的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
6.如果a>b>0,那么下列不等式中不正确的是( )
| A. | ab>b2 | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | $\frac{1}{a}$<$\frac{1}{b}$ | D. | a2>ab |