题目内容
17.利用余弦函数图象,写出满足cosx>0的x的区间是(-$\frac{π}{2}$+2kπ,$\frac{π}{2}$+2kπ),(k∈Z).分析 由条件利用余弦函数的图象,求得满足cosx>0的x的区间.
解答 解:结合余弦函数y=cosx的图象,由cosx>0,
可得x∈(-$\frac{π}{2}$+2kπ,$\frac{π}{2}$+2kπ),(k∈Z),
故答案为:(-$\frac{π}{2}$+2kπ,$\frac{π}{2}$+2kπ),k∈Z.
点评 本题主要考查余弦函数的图象特征,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
5.若某程序框图如图所示,则该程序运行后输出S的值为( )
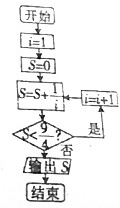

| A. | $\frac{147}{60}$ | B. | $\frac{17}{6}$ | C. | $\frac{25}{4}$ | D. | $\frac{137}{60}$ |
12.已知全集U=R,集合M={x|log${\;}_{\frac{1}{2}}$(x-1)>-1},N={x|1<2x<4},则(∁UM)∩N=( )
| A. | {0|0<x≤3} | B. | {x|1<x≤3} | C. | {x|0<x≤1} | D. | {x|1<x<2} |
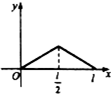
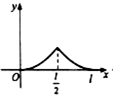
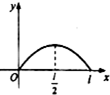
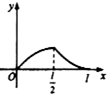
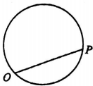 如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )
如图,点P从点O出发,按逆时针方向沿周长为l的圆周运动一周,则O,P两点连线的距离y与点P走过的路程x的函数图象可能是( )