题目内容
已知sin（α+β）=1，求证：tan（2α+β）+tanβ=0．[提示：注意角的变换：2α+β=2（α+β）-β]．
考点：二倍角的正切,两角和与差的正切函数
专题：三角函数的求值
分析：由于sin（α+β）=1，可得cos（α+β）=0．利用同角三角函数基本关系式、两角和差的正弦公式、倍角公式可得tan（2α+β）+tanβ=
+
=
=
即可证明．
| sin(2α+β) |
| cos(2α+β) |
| sinβ |
| cosβ |
| sin(2α+2β) |
| cos(2α+β)cosβ |
| 2isn(α+β)cos(α+β) |
| cos(2α+β)cosβ |
解答：
证明：∵sin（α+β）=1，
∴cos（α+β）=0．
∴tan（2α+β）+tanβ=
+
=
=
=
=0．
∴tan（2α+β）+tanβ=0．
∴cos（α+β）=0．
∴tan（2α+β）+tanβ=
| sin(2α+β) |
| cos(2α+β) |
| sinβ |
| cosβ |
| sin(2α+β)cosβ+cos(2α+β)sinβ |
| cos(2α+β)cosβ |
| sin(2α+2β) |
| cos(2α+β)cosβ |
=
| 2isn(α+β)cos(α+β) |
| cos(2α+β)cosβ |
∴tan（2α+β）+tanβ=0．
点评：本题考查了同角三角函数基本关系式、两角和差的正弦公式、倍角公式、特殊角的三角函数值，考查了推理能力与计算能力，属于基础题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
函数函数f（x）=cos（sinx）的最小正周期是（ ）
A、
| ||
| B、π | ||
| C、2m | ||
| D、4m |
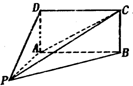如图，四棱锥P-ABCD的底面ABCD为矩形，且PA=AD=1，AB=2，∠PAB=120°，∠PBC=90°．