题目内容
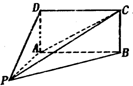如图，四棱锥P-ABCD的底面ABCD为矩形，且PA=AD=1，AB=2，∠PAB=120°，∠PBC=90°．（1）求证：平面PAD与平面PAB垂直；
（2）求直线PC与直线AB所成角的余弦值．（请用空间向量知识求解）
考点：异面直线及其所成的角,平面与平面垂直的判定
专题：空间位置关系与距离,空间角
分析：（1）利用线面垂直的判定定理可得BC⊥平面PAB．由于AD∥BC，可得AD⊥平面PAB，即可证明平面PAD与平面PAB垂直．
（2）建立空间直角坐标系，利用向量的夹角公式即可得出．
（2）建立空间直角坐标系，利用向量的夹角公式即可得出．
解答：
证明：（1）∵∠PBC=90°，∴BC⊥PB．
∵ABCD为矩形，∴BC⊥AB，
又AB∩PB=B，
∴BC⊥平面PAB．
∵AD∥BC，
∴AD⊥平面PAB，
∴平面PAD与平面PAB垂直．
（2）解：建立空间直角坐标系．
则A（0，0，0），B（0，2，0），C（0，2，1），P(
，-
，0)．
∴
=(-
，
，1)，
=（0，2，0）．
∴cos＜
，
＞=
=
=
．
∵ABCD为矩形，∴BC⊥AB，
又AB∩PB=B，
∴BC⊥平面PAB．
∵AD∥BC，
∴AD⊥平面PAB，
∴平面PAD与平面PAB垂直．
（2）解：建立空间直角坐标系．
则A（0，0，0），B（0，2，0），C（0，2，1），P(
| ||
| 2 |
| 1 |
| 2 |
∴
| PC |
| ||
| 2 |
| 5 |
| 2 |
| AB |
∴cos＜
| PC |
| AB |
| ||||
|
|
| 5 | ||
4
|
5
| ||
| 8 |
点评：本题考查了线面面面垂直的判定定理与性质定理、向量的夹角公式，属于基础题．
练习册系列答案
相关题目
双曲线16x2-9y2=144的离心率e=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|